
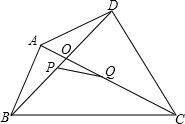
 如图所示.求证:任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍.
如图所示.求证:任意四边形四条边的平方和等于对角线的平方和加对角线中点连线平方的4倍. | BD |
| 2 |
| BD2 |
| 2 |
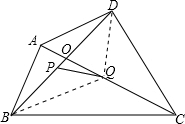
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
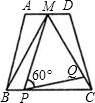 如图所示,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
如图所示,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
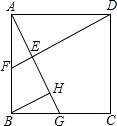 (2013•厦门)如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得AG=DE+HG,连接BH.求证:∠ABH=∠CDE.
(2013•厦门)如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得AG=DE+HG,连接BH.求证:∠ABH=∠CDE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com