
【题目】甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图是甲乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶. 
(1)甲车的速度是千米/小时;乙车速度是千米/小时;a= .
(2)甲车出发多长时间后两车相距330千米?
【答案】
(1)120;100; ![]()
(2)解:设直线BC的解析式为S=k1t+b1(k1≠0),
将B(1,440),C(3,0)代入得,
 ,
,
解得  ,
,
所以,S=﹣220t+660,
当﹣220t+660=330时,解得t=1.5,
直线CD的解析式为S=k2t+b2(k2≠0),
点D的横坐标为 ![]() +3=
+3= ![]() ,
,
将C(3,0),D( ![]() ,
, ![]() )代入得,
)代入得,  ,
,
解得  ,
,
所以,S=220t﹣660(3≤t≤ ![]() )
)
当220t﹣660=330时,解得t=4.5,
答:甲出发1.5小时或4.5小时后两车相距330千米.

【解析】解:(1)t=0时,S=560,
所以,M、N两地的距离为560千米;
甲车的速度为:(560﹣440)÷1=120km/h,
设乙车的速度为xkm/h,
则(120+x)×(3﹣1)=440,
解得x=100;
相遇后甲车到达N地的时间为:(3﹣1)×100÷120= ![]() (小时),
(小时),
所以,a=(120+100)× ![]() =
= ![]() 千米;
千米;
所以答案是:120,100, ![]() ;
;


科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线![]() 在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线![]() 上运动,则k的值是 .
上运动,则k的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
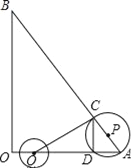
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线①y=2x2;②y=2(x+1)2﹣5;③y=3(x+1)2;④y=(x+1)2﹣5.其中, 形状相同的是( )
A. ①② B. ②③④ C. ②④ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不确定事件发生的可能性未必是50%,可能大些,也可能小些,试按发生的可能性由大到小的顺序,把下列事件排列起来.
事件一:我的书包里共有12本书,我随便把手往里一伸,恰好摸到数学书(假设书都同样厚).
事件二:我花2元钱买了一张彩票,中了大奖,得500万元奖金.
事件三:我抛了两次硬币,每次都是正面向上.
事件四:这天早晨,我第一个来到教室.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com