
【题目】将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(﹣2,1).
(1)求△ABC的面积S;
(2)求直线AB与y轴的交点坐标.
【答案】解:(1)过点A作AD⊥x轴,垂足为D.
∵C(1,0),A(﹣2,1),
∴AD=1,DC=1﹣(﹣2)=3,
∴AC2=AD2+DC2=10,
∴S△ABC=![]() AC2=5;
AC2=5;
(2)过点B作BE⊥x轴,垂足为E,
∴∠ADC=∠CEB=90°,
∴∠CAD+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠CAD=∠BCE.
在△ADC和△CEB中,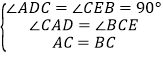 ,
,
∴△ADC≌△CEB,
∴CD=BE=3,CE=AD=1,
∴OE=2,
∴点B的坐标为(2,3).
设直线AB的解析式为y=kx+b,则![]() ,
,
解得![]() ,
,
∴y=![]() x+2.
x+2.
当x=0时,y=2,
∴直线AB交y轴于点(0,2).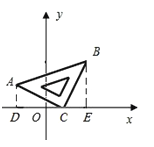
【解析】(1)过点A作AD⊥x轴,垂足为D,根据A、C两点的坐标可求出AD和DC,根据勾股定理可求出AC2 , 即可求出等腰直角△ABC的面积;
(2)要求直线AB与y轴的交点坐标,只需求出直线AB的解析式,只需求出点B的坐标,过点B作BE⊥x轴,垂足为E,易证△ADC≌△CEB,即可得到BE和CE,
从而得到点B的坐标,问题得以解决.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】图①是一面矩形彩旗完全展平时的尺寸图(单位:cm),其中矩形ABCD是由双层白布缝制的穿旗杆用的旗裤,阴影部分DCEF为矩形绸缎旗面.
(1)用经加工的圆木杆穿入旗裤作旗杆,求旗杆的最大直径(精确到1cm);
(2)将穿好彩旗的旗杆垂直插在操场上,旗杆从旗顶到地面的高度为220cm,在无风的天气里,彩旗自然下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.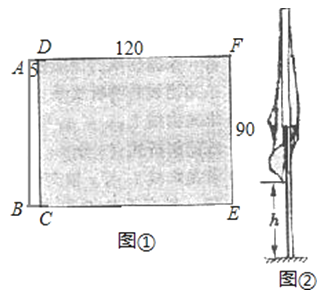
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场新进一批空调,按进价提高30 %后标价.五一期间,商场为了促销,又按标价打九折销售,每台空调仍可获利680元,该批空调每台的进货价格为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要表示一个家庭一年用于“教育”, “服装”,“食品”,“其他”这四项的支出各占家庭本年总支出的百分比,从“扇形统计图”,“条形统计图”,“折线统计图”中选择一种统计图,最适合的统计图是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )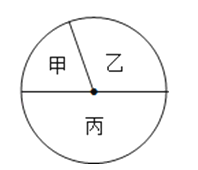
A.扇形甲的圆心角是72°
B.学生的总人数是90人
C.初三的人数比初二的人数多10人
D.初一的人数比初三的人数少15人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4.点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动.当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).

(1)求tanB的值.
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为两部分时,设这两部分的面积比为k.当![]() 时,直接写出t的取值范围.
时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“人人会乐器”的活动,根据实际开设了四种乐器的相关课程.学校为了了解学生最喜欢哪一种乐器(每位学生只能选一类),随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图. 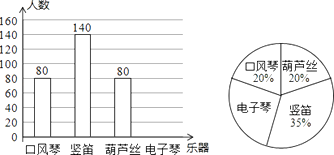
请你根据图中提供的信息,回答下列问题:
(1)总共随机抽查了多少位学生?请你把条形统计图补全.
(2)样本中喜欢电子琴的人数比喜欢葫芦丝的多人.
(3)该校一共有2000名学生,你认为全校喜欢哪种乐器的学生人最多?估计有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com