
【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4.点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动.当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).

(1)求tanB的值.
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为两部分时,设这两部分的面积比为k.当![]() 时,直接写出t的取值范围.
时,直接写出t的取值范围.
【答案】(1)![]() ;(2)当点M落在BC边上时,t=
;(2)当点M落在BC边上时,t=![]() .
.
(3)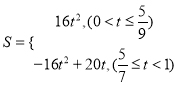 ;
;
(4)![]() <t≤
<t≤![]() ,1≤t<
,1≤t<![]()
【解析】试题分析:(1)根据勾股定理求出AD的长,然后可求的BD,代入锐角三角函数即可求解;
(2)当点M落在BC边上时, PQ=PN=MN=4t, BN=2t,然后列方程求解即可;
(3)分两种情况:当0<t≤![]() 时,当
时,当![]() ≤t<1时,分别求面积即可;
≤t<1时,分别求面积即可;
(4)根据上面所求直接判断即可.
试题解析:(1)∵CD⊥AB,
∴∠ADC=∠ADB= 90°.
∵在Rt△ACD中, ![]() ,
,
∴BD=AB-AD=5-3=2.
∴在Rt△BCD中, ![]() .
.
(2)当点M落在BC边上时, PQ=PN=MN=4t, BN=2t.
∴3t+4t+2t=5,
∴t=![]() .
.
(3)当0<t≤![]() 时,S=16t.
时,S=16t.
当![]() ≤t<1时,
≤t<1时, ![]() .
.
(4)![]() <t≤
<t≤![]() ,1≤t<
,1≤t<![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图l,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
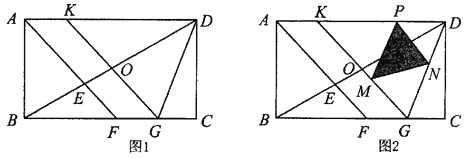
(1)求证:△DOK≌△BOG;
(2)求证:AB+AK=BG:
(3)如图2,若KD=KG=2,点P是线段KD上的动点(不与点D、K重台),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=x,S△PMN=y,求出y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将等腰直角△ABC斜放在平面直角坐标系中,使直角顶点C与点(1,0)重合,点A的坐标为(﹣2,1).
(1)求△ABC的面积S;
(2)求直线AB与y轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】银川市某天的气温是7℃~﹣3℃.则计算这天温差的算式( )
A. (7﹣3)℃ B. (7+3)℃ C. (﹣3﹣7)℃ D. [7﹣(﹣3)]℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )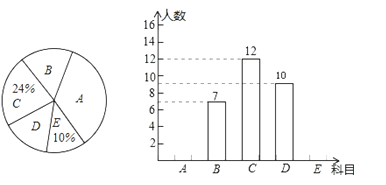
A.选科目E的有5人
B.选科目D的扇形圆心角是72°
C.选科目A的人数占体育社团人数的一半
D.选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“迎新年,庆元旦”期间,某商场推出A、B、C、D四种不同类型礼盒共1000盒进行销售,在图1中是各类型礼盒所占数的百分比,已知四类礼盒一共已经销售了50%,各类礼盒的销售数量如图2所示: 
(1)商场中的D类礼盒有盒.
(2)请在图1扇形统计图中,求出A部分所对应的圆心角等于度.
(3)请将图2的统计图补充完整.
(4)通过计算得出类礼盒销售情况最好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com