
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上. 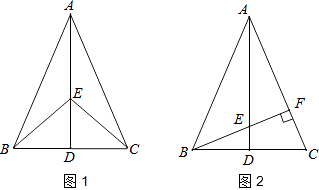
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
【答案】
(1)证明:∵AB=AC,D是BC的中点,
∴∠BAE=∠EAC,
在△ABE和△ACE中, 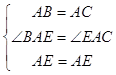 ,
,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)证明:∵∠BAC=45°,BF⊥AF,
∴△ABF为等腰直角三角形,
∴AF=BF,
∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,
∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中, 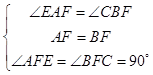 ,
,
∴△AEF≌△BCF(ASA)
【解析】(1)根据等腰三角形三线合一的性质可得∠BAE=∠EAC,然后利用“边角边”证明△ABE和△ACE全等,再根据全等三角形对应边相等证明即可;(2)先判定△ABF为等腰直角三角形,再根据等腰直角三角形的两直角边相等可得AF=BF,再根据同角的余角相等求出∠EAF=∠CBF,然后利用“角边角”证明△AEF和△BCF全等即可.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①②成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”. 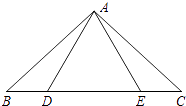
(1)以上三个命题是真命题的为(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品原售价200元,由于产品换代,现连续两次降价处理,按72元的售价销售.已知两次降价的百分率相同,若设降价的百分率为x,则可列出方程为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
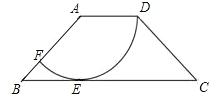
【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
(1)求∠ABE的大小及![]() 的长度;
的长度;
(2)在BE的延长线上取一点G,使得![]() 上的一个动点P到点G的最短距离为
上的一个动点P到点G的最短距离为![]() ,求BG的长.
,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个变量x、y不是反比例的关系是( )
A.书的单价为12元,售价y(元)与书的本数x(本)
B.xy=7
C.当k=﹣1时,式子![]() 中的y与x
中的y与x
D.小亮上学用的时间x(分钟)与速度y(米/分钟)
查看答案和解析>>
科目:初中数学 来源: 题型:
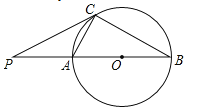
【题目】如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
(1)求证:∠PCA=∠B;
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com