
 如图,P为⊙O的直径EF延长线上一点,PA交⊙O于B、A两点,PC交⊙O于点D、C两点,且AB=CD,求证:
如图,P为⊙O的直径EF延长线上一点,PA交⊙O于B、A两点,PC交⊙O于点D、C两点,且AB=CD,求证: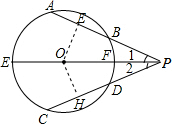 (1)证明:过点O分别作OE⊥AB,OH⊥CD于点E、H,
(1)证明:过点O分别作OE⊥AB,OH⊥CD于点E、H,
|


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
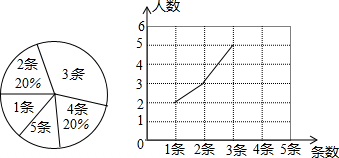
 某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论:
某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论:| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
 |
| NF |
| PG-PF |
| NP |
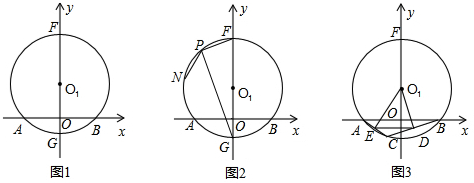
查看答案和解析>>
科目:初中数学 来源: 题型:
 某市出租车管理处公示的出租车运价如图:
某市出租车管理处公示的出租车运价如图:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
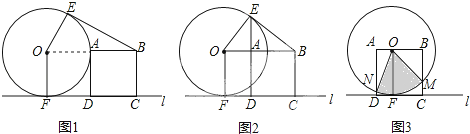
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,点A、B、C的坐标分别为(2,0)、(1,2)、(3,4),直线l的解析式为:y=kx+4-3k(k≠0).
如图,在平面直角坐标系中,点A、B、C的坐标分别为(2,0)、(1,2)、(3,4),直线l的解析式为:y=kx+4-3k(k≠0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com