练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】观察下列式子：，，，，…．

    （1）仿照上面的例子，写出第6个式子为：；

    （2）由此猜想，第个式子是什么？并证明你的猜想．

    【答案】（1）4221；（2），证明见解析

    【解析】

    (1)观察所给式子，不难发现：13×17=100×1×2+3×7=221；23×27=100×2×3+3×7=621…，按此规律求解即可；

    (2)根据(1)中的算式，猜想第个式子是，利用多项式乘以多项式的运算法则即可证明．

    (1) 观察所给式子，不难发现：

    13×17=100×1×2+3×7=221，

    23×27=100×2×3+3×7=621，

    …，

    ∴63×67=100×6×7+3×7=4221，

    故答案为：；

    (2)由此猜想，第个式子为：，

    左边=

    =

    =右边，

    所以，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】随着科技的进步和网络资源的丰富，在线学习已经成为更多人的自主学习选择．某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论．为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图．

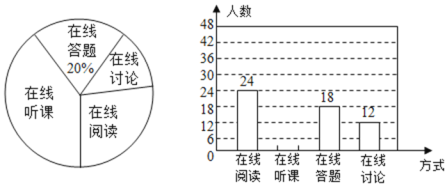
    （1）求本次调查的学生总人数，并补全条形统计图；

    （2）求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

    （3）该校共有学生3000人，请你估计该校对在线阅读最感兴趣的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】O为直线AB上的一点，OC⊥OD，射线OE平分∠AOD.

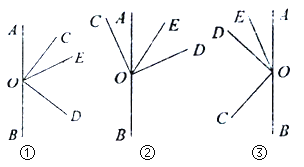
    (1)如图①，判断∠COE和∠BOD之间的数量关系，并说明理由；

    (2)若将∠COD绕点O旋转至图②的位置，试问(1)中∠COE和∠BOD之间的数量关系是否发生变化？并说明理由；

    (3)若将∠COD绕点O旋转至图③的位置，探究∠COE和∠BOD之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，．点从点出发沿方向以每秒个单位长的速度向点匀速运动，同时点从点出发沿方向以每秒个单位长的速度向点匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点、运动的时间是秒（）．过点作于点，连接、．

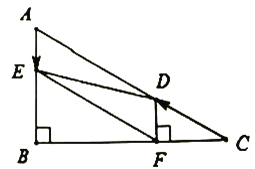
    （1）的长是 ，的长是 ；

    （2）在、的运动过程中，线段与的关系是否发生变化？若不变化，那么线段与是何关系，并给予证明；若变化，请说明理由．

    （3）四边形能够成为菱形吗？如果能，求出相应的值；如果不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知∠ACD是△ABC的一个外角，我们容易证明∠ACD＝∠A+∠B，即三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？

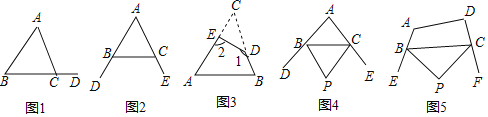
    尝试探究：（1）如图2，∠DBC与∠ECB分别为△ABC的两个外角，则∠DBC+∠ECB　　∠A+180°（横线上填＞、＜或＝）

    初步应用：（2）如图3，在△ABC纸片中剪去△CED，得到四边形ABDE，∠1＝135°，则∠2－∠C＝　　　　　．

    解决问题：（3）如图4，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请利用上面的结论直接写出答案　　　　　　．

    （4）如图5，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，请利用上面的结论探究∠P与∠A、∠D的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

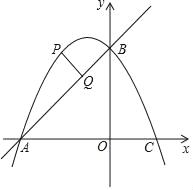
    【题目】如图，在平面直角坐标系中，直线y=x+2与坐标轴交于A、B两点，点A在x轴上，点B在y轴上，C点的坐标为（1，0），抛物线y=ax2+bx+c经过点A、B、C．

    （1）求该抛物线的解析式；

    （2）根据图象直接写出不等式ax2+（b﹣1）x+c＞2的解集；

    （3）点P是抛物线上一动点，且在直线AB上方，过点P作AB的垂线段，垂足为Q点．当PQ=时，求P点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售，当此农产品售价为每袋36元时，3月份销售125袋，4、5月份该农产品十分畅销，销售量持续走高.在售价不变的基础上，5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.

    （1）求4、5这两个月销售量的月平均增长率；

    （2）6月份起，该商店采用降价促销的方式回馈顾客，经调查发现，该农产品每降价1元/袋，销量就增加4袋，当农产品每袋降价多少元时，该商店6月份获利1920元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将两块直角三角尺的直角顶点C叠放在一起．

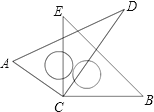
    （1）判断∠ACE与∠BCD的大小关系，并说明理由；

    （2）若∠DCE=30°，求∠ACB的度数；

    （3）猜想：∠ACB与∠DCE有怎样的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平面上四个点.

    （1）按下列要求画图（不写画法）

    ①连接，；②作直线；③作射线，交于点.

    （2）在（1）所画的图形中共有__________条线段，__________条射线. （所画图形中不能再添加标注其他字母）；

    （3）通过测量线段，，，可知__________（填“”，“”或“”），可以解释这一现象的基本事实为：_______________________.

    查看答案和解析>>

    同步练习册答案