
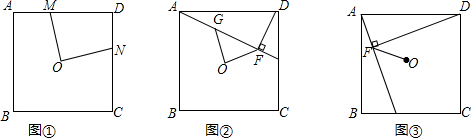
分析 (1)利用正方形的性质得到∠OAM=∠ODM,再利用等量的差相等得到∠AOM=∠DON,从而证明出△AOM≌△DON即可,
(2)利用正方形的性质得到∠OAM=∠ODM,再利用等量的和相等得到∠DAE=∠FDE,从而证明出△OAG≌△ODF即可,
(3)借助与(1)和(2)的特点作出辅助线即可.
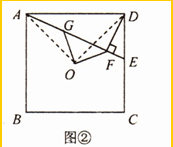
解答 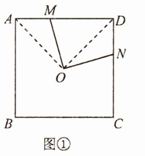 (1)证明:如图①,连接OA,OD,则OA=OD,
(1)证明:如图①,连接OA,OD,则OA=OD,
∵四边形ABCD是正方形,
∴∠AOD=90°,
∠OAM=∠ODM=45°,
∵∠MON=90°,
∴∠AOD-∠MOD=∠MON-∠MOD,
∴∠AOM=∠DON,
∴△AOM≌△DON(ASA),
∴OM=ON;
(2)
如图②,△OFG为等腰直角三角形.
证明:连接OA,OD,则OA=OD,
∵四边形ABCD是正方形,
∴∠AOD=90°,
∠OAD=∠ODC=45°,
∵DF⊥AE,
∴∠DAE+∠ADF=∠ADF+FDE=90°
∴∠DAE=∠FDE,
∴∠OAG=∠ODF,
∵AG=DF,
∴△OAG≌△ODF,
∴OG=OF,
∠AOG=∠DOF,
∴∠GOF=∠GOD+∠DOF=∠AOG+∠GOD=90°,
故△OFG为等腰直角三角形.
(3)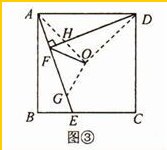
解:如图③,在AE上截取AG=DF,连接OA,OD,OG,其中OA与DF交于点H,则AO=DO,
∵∠AFD=∠AOD=90°,
∠AHF=∠DHO,
∴∠GAO=∠FDO,
∴△OAG≌△ODF,
∴OG=OF,
∠AOG=∠DOF,
∴∠GOF=∠GOA-∠FOA=∠DOF-∠FOA=90°,
∴∠GFO=45°,
∴DF⊥AE,
∴∠DFO=45°.
点评 本题是四边形的综合题,主要考查了正方形的性质,涉及到正方形正方形的对角线垂直相等且平分,如OA=OD,用到等量的和(差)相等,如得到∠AOM=∠DON,∠DAE=∠FDE,本题的关键是充分利用正方形的性质.


科目:初中数学 来源: 题型:填空题
| 波长(m) | 300 | 500 | 600 | 1000 | 1500 |
| 频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
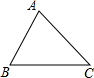 如图,△ABC是锐角三角形,sinC=$\frac{4}{5}$,则sinA的取值范围是( )
如图,△ABC是锐角三角形,sinC=$\frac{4}{5}$,则sinA的取值范围是( )| A. | 0$<sinA<\frac{3}{5}$ | B. | $\frac{4}{5}<sinA<1$ | C. | $\frac{3}{5}<sinA<\frac{4}{5}$ | D. | $\frac{3}{5}<sinA<1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com