
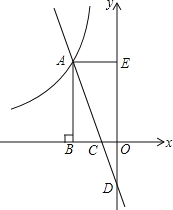
【题目】如图,直线y=kx﹣2与双曲线y=-![]() (x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E, △ABC的面积为2.
(x<0)交于点A,与x轴交于点C,与y轴交于点D.AB⊥x轴于点B,AE⊥y轴于点E, △ABC的面积为2.
(1)直接写出四边形OCAE的面积;
(2)求点C的坐标.
【答案】(1)四边形OCAE的面积为4;(2)C(﹣![]() ,0).
,0).
【解析】(1)根据反比例函数系数k的几何意义即可求得;(2)设A(x,-![]() ),根据△ABC的面积为2,求得BC= -
),根据△ABC的面积为2,求得BC= -![]() x,OC=-
x,OC=-![]() x,根据△ABC∽△DOC求得
x,根据△ABC∽△DOC求得![]() ,由直线的解析式求得D的坐标为(0,-2)得出OD=2,从而求得AB=4,代入反比例函数解析式求得A的坐标,求得OB的长,即可求得C的坐标.
,由直线的解析式求得D的坐标为(0,-2)得出OD=2,从而求得AB=4,代入反比例函数解析式求得A的坐标,求得OB的长,即可求得C的坐标.
(1)∵双曲线为y=﹣![]() (x<0),
(x<0),
∴四边形ABOE的面积为6,
∵△ABC的面积为2.
∴四边形OCAE的面积为4.
(2)∵A点是双曲线y=﹣![]() (x<0)上的点,
(x<0)上的点,
设A(x,﹣![]() ),
),
∴AB=﹣![]() ,
,
∵△ABC的面积为2.
∴![]() ABBC=2,即
ABBC=2,即![]() ×(﹣
×(﹣![]() )BC=2
)BC=2
∴BC=﹣![]() x,
x,
∴OC=﹣![]() x,
x,
∵AB⊥x轴于点B,
∴AB∥y轴,
∴△ABC∽△DOC,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
由直线y=kx﹣2可知D(0,﹣2),
∴OD=2,
∴AB=4,
∴﹣![]() =4,解得x=﹣
=4,解得x=﹣![]() ,
,
∴A(﹣![]() ,4),
,4),
代入![]() k﹣2,解得k=﹣4,
k﹣2,解得k=﹣4,
∴直线:y=﹣4x﹣2,
令y=0,则x=﹣![]() ,
,
∴C(﹣![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
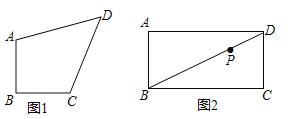
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0)、C(0,﹣3).
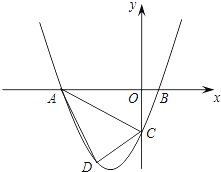
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?如存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
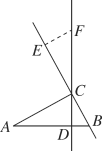
【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)当点E运动多长时间时,CF=AB.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠BAC=90°,AB=AC,点P为AC上一点,M为BC上一点.
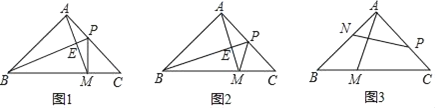
(1)若AM⊥BP于点E.
①如图1,BP为△ABC的角平分线,求证:PA=PM;
②如图2,BP为△ABC的中线,求证:BP=AM+MP.
(2)如图3,若点N在AB上,AN=CP,AM⊥PN,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
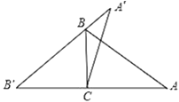
【题目】如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′为AC延长线上一点,A′是B′B延长线上一点,△A′B′C≌△ABC,则∠BCA′:∠BCB′=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com