练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

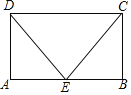
    【题目】如图，在矩形ABCD中，E是AB的中点，连接DE、CE．

    （1）求证：△ADE≌△BCE；

    （2）若AB=6，AD=4，求△CDE的周长．

    【答案】（1）证明见解析；（2）16.

    【解析】（1）由全等三角形的判定定理SAS即可证得结论；

    （2）由（1）中全等三角形的对应边相等和勾股定理求得线段DE的长度，结合三角形的周长公式解答．

    （1）在矩形ABCD中，AD=BC，∠A=∠B=90°．

    ∵E是AB的中点，

    ∴AE=BE，

    在△ADE与△BCE中，

    ，

    ∴△ADE≌△BCE（SAS）；

    （2）由（1）知：△ADE≌△BCE，则DE=EC，

    在直角△ADE中，AE=4，AE=AB=3，

    由勾股定理知，DE==5，

    ∴△CDE的周长=2DE+AD=2DE+AB=2×5+6=16．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

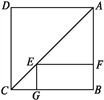
    【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.

    (1)求证:四边形BFEG是矩形;

    (2)求四边形EFBG的周长;

    (3)当AF的长为多少时,四边形BFEG是正方形?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

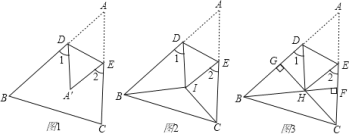
    【题目】（1）如图1，把△ABC沿DE折叠，使点A落在点A’处，若∠A=50°，求∠1+∠2的度数，猜想并直接写出∠1+∠2与∠A的数量关系．（不必证明）

    （2）如图2，BI平分∠ABC，CI平分∠ACB，把△ABC折叠，使点A与点I重合，若∠1+∠2=110°，求∠BIC的度数；

    （3）如图3，在锐角△ABC中，BF⊥AC于点F，CG⊥AB于点G，BF、CG交于点H，把△ABC折叠使点A和点H重合，试探索∠BHC与∠1+∠2的关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

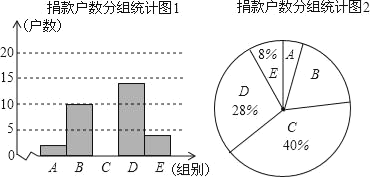
    【题目】为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动．对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图和统计表(图中信息不完整)．已知A、B两组捐款户数的比为1：5．请结合以上信息解答下列问题．捐款户数分组统计表

    组别

    捐款额(x)元

    户数

    A

    1≤x＜50

    a

    B

    50≤x＜100

    10

    C

    100≤x＜150

    　 　

    D

    150≤x＜200

    　 　

    E

    x≥200

    　 　

    (1)a＝　 　，本次调查样本的容量是　 　；

    (2)补全“捐款户数分组统计图1和捐款户数分组统计表”；

    (3)若该社区有2000户住户，请根据以上信息，估计全社区捐款不少于150元的户数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，坐标原点O是菱形ABCD的对称中心．边AB与x轴平行，点B（1，-2），反比例函数 （k≠0）的图象经过A，C两点．

    （1）求点C的坐标及反比例函数的解析式．
    （2）直线BC与反比例函数图象的另一交点为E，求以O，C，E为顶点的三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校研究性学习小组在学习二次根式 =|a|之后，研究了如下四个问题，其中错误的是（ ）
    A.在a＞1的条件下化简代数式a+ 的结果为2a﹣1
    B.当a+ 的值恒为定值时，字母a的取值范围是a≤1
    C.a+ 的值随a变化而变化，当a取某个数值时，上述代数式的值可以为
    D.若 =（ ）2 ， 则字母a必须满足a≥1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读与计算：请阅读以下材料，并完成相应的任务． 古希腊的几何学家海伦在他的《度量》一书中给出了利用三角形的三边求三角形面积的“海伦公式”：如果一个三角形的三边长分别为a、b、c，设p= ，则三角形的面积S= ．
    我国南宋著名的数学家秦九韶，曾提出利用三角形的三边求面积的“秦九韶公式”（三斜求积术）：如果一个三角形的三边长分别为a、b、c，则三角形的面积S= ．
    （1）若一个三角形的三边长分别是5，6，7，则这个三角形的面积等于 ．
    （2）若一个三角形的三边长分别是 ，求这个三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：已知AB∥CD，∠ABE与∠CDE两个角的角平分线相交于F．

    （1）如图1，若∠E=80°，求∠BFD的度数．

    （2）如图2：若∠ABM=∠ABF，∠CDM=∠CDF，写出∠M和∠E之间的数量关系并证明你的结论．

    （3）若∠ABM＝∠ABF, ∠CDM＝∠CDF, 设∠E＝m°,直接用含有n、m°的代数式写出∠M＝ (不写过程)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】向日葵水果店推出甲乙两种礼盒，甲礼盒中有樱桃千克，枇杷千克，香梨千克，乙礼盒中有樱桃千克，枇杷千克，哈蜜瓜千克，己知樱桃每千克元，甲礼盒每盒元，乙礼盒每盒元，当然，顾客也可根据需要自由搭配，小陶用元买乙礼盒和自由搭配礼盒(香梨千克，枇杷千克，哈蜜瓜千克)若干盒，则小陶一共可买礼盒____个．

    查看答案和解析>>

    同步练习册答案