
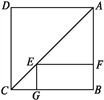
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
【答案】(1)见解析;(2)20cm(3)当AF=5 cm时,四边形BFEG是正方形.
【解析】(1)由正方形的性质可得出AB⊥BC、∠B=90°,根据EF⊥AB、EG⊥BC利用“垂直于同一条直线的两直线互相平行”,即可得出EF∥GB、EG∥BF,再结合∠B=90°,即可证出四边形BFEG是矩形;
(2)由正方形的周长可求出正方形的边长,根据正方形的性质可得出△AEF为等腰直角三角形,进而可得出AF=EF,再根据矩形的周长公式即可求出结论;
(3)由正方形的判定可知:若要四边形BFEG是正方形,只需EF=BF,结合AF=EF、AB=10cm,即可得出结论.
(1)证明:∵四边形ABCD为正方形,
∴AB⊥BC,∠B=90°.
∵EF⊥AB,EG⊥BC,
∴EF∥GB,EG∥BF.
∵∠B=90°,
∴四边形BFEG是矩形;
(2)∵正方形ABCD的周长是40cm,
∴AB=![]() =10cm.
=10cm.
∵四边形ABCD为正方形,
∴△AEF为等腰直角三角形,
∴AF=EF,
∴四边形EFBG的周长C=2(EF+BF)=2(AF+BF)=20cm.
(3)若要四边形BFEG是正方形,只需EF=BF,
∵AF=EF,AB=10cm,
∴当AF=5cm时,四边形BFEG是正方形.


科目:初中数学 来源: 题型:
【题目】已知点P是直线![]() 上一定点,点A是x轴上一动点
上一定点,点A是x轴上一动点![]() 不与原点重合
不与原点重合![]() ,连接PA,过点P作
,连接PA,过点P作![]() ,交y轴于点B,探究线段PA与PB的数量关系.
,交y轴于点B,探究线段PA与PB的数量关系.

![]() 1
1![]() 如图
如图![]() ,当
,当![]() 轴时,观察图形发现线段PA与PB的数量关系是______;
轴时,观察图形发现线段PA与PB的数量关系是______;
![]() 2
2![]() 当PA与x轴不垂直时,在图
当PA与x轴不垂直时,在图![]() 中画出图形,线段PA与PB的数量关系是否与
中画出图形,线段PA与PB的数量关系是否与![]() Ⅰ
Ⅰ![]() 所得结果相同?写出你的猜想并加以证明;
所得结果相同?写出你的猜想并加以证明;
![]() 3
3 ![]() 为何值时,线段
为何值时,线段![]() ?此时
?此时![]() 的度数是多少,为什么?
的度数是多少,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个实际问题的函数图象的形状与y= ![]() 的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为( ).
的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为( ).
A.y= ![]()
B.y= ![]() 或y=
或y= ![]()
C.y= ![]()
D.y= ![]() 或y=
或y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
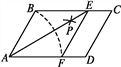
【题目】如图,在ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证:四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=![]() ,求∠C的大小.
,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3.
<3.
∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2,
﹣2,
∴1<![]() ﹣1<2
﹣1<2
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
解决问题:已知:a是![]() ﹣3的整数部分,b是
﹣3的整数部分,b是![]() ﹣3的小数部分,
﹣3的小数部分,
求:(1)a,b的值;
(2)(﹣a)3+(b+4)2的平方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2-2mx-3 , 有下列说法:
①它的图象与x轴有两个公共点;
②如果当x≤1时y随x的增大而减小,则m=1;
③如果将它的图象向左平移3个单位后过原点,则m=-1;
④如果当x=4时的函数值与x=2008时的函数值相等,则当x=2012时的函数值为-3 .
其中正确的说法是 . (把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投出多少个3分球?共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7﹣∠8的值是( )

A. 600° B. 700° C. 720° D. 800°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com