
【题目】如图,在ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证:四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=![]() ,求∠C的大小.
,求∠C的大小.
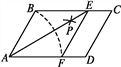
【答案】(1)见解析;(2)60°
【解析】(1)先证四边形ABEF是平行四边形,再根据AB=BE即可证明平行四边形ABEF是菱形;
(2)连接BF交AE于G,由菱形的性质得出AB、AG的长,再由勾股定理求出BG的长,即可证三角形ABF为等边三角形,最后求出∠C的度数.
证明:在△APB和△APF中,
∵AB=AF,BP=FP,AP=AP,
∴△APB≌△APF.
∴∠EAB=∠EAF.
∵AD∥BC,
∴∠EAF=∠AEB=∠EAB.
∴BE=AB=AF.
∵AF∥BE,
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形.
(2)解:如图,连接BF,交AE于G.
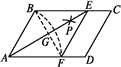
∵菱形ABEF的周长为16,AE=4![]() ,
,
∴AB=BE=EF=AF=4,AG=![]() AE=2
AE=2![]() ,∠BAF=2∠BAE,AE⊥BF,
,∠BAF=2∠BAE,AE⊥BF,
在Rt△ABG中,GB=![]() =
=![]() =2,
=2,
∴BF=2BG=4.
∴AB=AF=BF=4.
∴△ABF是等边三角形.
∴∠BAF=60°.
∴∠C=∠BAF=60°.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连接DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.
(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若y= ![]() ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
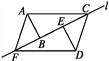
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
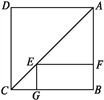
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦假期,小明一家游览仓圣公园,公园内有一座假山,假山上有一条石阶小路,其中有两段台阶的高度如图所示(图中的数字表示每一级台阶的高度,单位:cm).请你运用所学习的统计知识,解决以下问题:
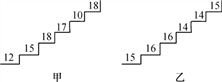
(1)把每一级台阶的高度作为数据,请从统计知识方面(平均数、中位数)说一下甲、乙两段台阶有哪些相同点和不同点?
(2)甲、乙两段台阶哪段上行走会比较舒服?你能用所学知识说明吗?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列做法正确的是( )
A. 由2(x+1)=x+7去括号、移项、合并同类项,得x=5
B. 由![]() =1+
=1+![]() 去分母,得2(2x﹣1)=1+3(x﹣3)
去分母,得2(2x﹣1)=1+3(x﹣3)
C. 由2(2x﹣1)﹣3(x﹣3)=1去括号,得4x﹣2﹣3x﹣9=1
D. 由7x=4x﹣3移项,得7x﹣4x=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:
①∠A+∠B=∠C
②∠A:∠B:∠C=1:2:3
③∠A= ![]() ∠B=
∠B= ![]() ∠C
∠C
④∠A=∠B=2∠C 中,能确定△ABC 为直角三角形的条件有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com