
【题目】某校研究性学习小组在学习二次根式 ![]() =|a|之后,研究了如下四个问题,其中错误的是( )
=|a|之后,研究了如下四个问题,其中错误的是( )
A.在a>1的条件下化简代数式a+ ![]() 的结果为2a﹣1
的结果为2a﹣1
B.当a+ ![]() 的值恒为定值时,字母a的取值范围是a≤1
的值恒为定值时,字母a的取值范围是a≤1
C.a+ ![]() 的值随a变化而变化,当a取某个数值时,上述代数式的值可以为
的值随a变化而变化,当a取某个数值时,上述代数式的值可以为 ![]()
D.若 ![]() =(
=( ![]() )2 , 则字母a必须满足a≥1
)2 , 则字母a必须满足a≥1
科目:初中数学 来源: 题型:
【题目】为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型 | 乙型 | |
价格(元/台) | a | b |
有效半径(米/台) | 150 | 100 |
(1)求a、b的值;
(2)若购买该批设备的资金不超过11000元,且要求监控半径覆盖范围不低于1600米,两种型号的设备均要至少买一台,请你为学校设计购买方案,并计算最低购买费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第100个图中共有点的个数是

A. 15151B. 15152C. 15153D. 15154
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(a,0),C(0,c)且满足:(a+6)2+![]() =0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
=0,长方形ABCO在坐标系中(如图),点O为坐标系的原点.
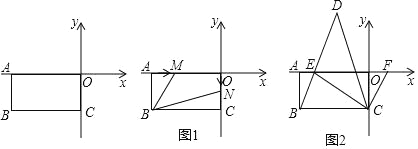
(1)求点B的坐标.
(2)如图1,若点M从点A出发,以2个单位/秒的速度向右运动(不超过点O),点N从原点O出发,以1个单位/秒的速度向下运动(不超过点C),设M、N两点同时出发,在它们运动的过程中,四边形MBNO的面积是否发生变化?若不变,求其值;若变化,求变化的范围.
(3)如图2,E为x轴负半轴上一点,且∠CBE=∠CEB,F是x轴正半轴上一动点,∠ECF的平分线CD交BE的延长线于点D,在点F运动的过程中,请探究∠CFE与∠D的数量关系,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,
证明:过点C作CF∥AB.

∵AB∥CF(已知),
∴∠B= ( ).
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ( )
∴∠2+ =180° ( )
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com