
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
【答案】(1)作图见解析(2)5;(3)作图见解析,A1(0,-4)、B1(2,-4)、C1.(3,1).
【解析】试题分析:(1)根据三点的坐标,在直角坐标系中分别标出位置即可.
(2)以AB为底,则点C到AB得距离即是底边AB的高,结合坐标系可得出高为点C的纵坐标的绝对值加上点B的纵坐标的绝对值,从而根据三角形的面积公式计算即可.
(3)关于x轴对称的点的坐标,横坐标不变,纵坐标互为相反数,从而可得出A1、B1、C1的坐标.
试题解析:(1)如图所示:
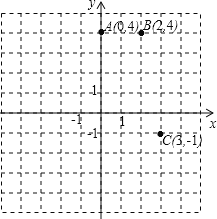
(2)由图形可得:AB=2,AB边上的高=|-1|+|4|=5,
∴△ABC的面积=![]() AB×5=5.
AB×5=5.
(3)∵A(0,4),B(2,4),C(3,-1),△A1B1C1与△ABC关于x轴对称,
∴A1(0,-4)、B1(2,-4)、C1.(3,1).


科目:初中数学 来源: 题型:
【题目】有下列图形,①三角形,②长方形,③平行四边形,④立方体,⑤圆锥,⑥圆柱,⑦圆,⑧球体,其中是平面图形的个数为( )
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,DB=DC,
(1)求证:AD平分∠BAC;
(2)延长CD与AB的延长线交于E ,延长AD到F,使DF=DC,连接EF,若∠C=100°,∠BAC=40°,求证:△EBD≌△EFD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是( )
A. AB∥CD,AB=CD B. AB∥CD,BC∥AD C. AB∥CD,BC=AD D. AB=CD,BC=AD
查看答案和解析>>
科目:初中数学 来源: 题型:
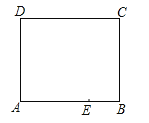
【题目】如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com