
【题目】如图,AB=AC,DB=DC,
(1)求证:AD平分∠BAC;
(2)延长CD与AB的延长线交于E ,延长AD到F,使DF=DC,连接EF,若∠C=100°,∠BAC=40°,求证:△EBD≌△EFD.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)易证△ABD≌△ACD,由此可得∠1=∠2,即AD平分∠BAC;
(2)由△ABD≌△ACD得∠1=∠2,∠ADB=∠ADC,即可证明△BDE≌△FDE.
试题解析:(1)证明:在△ABD和△ACD中,
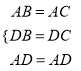 ,
,
∴ △ABD≌△ACD,
∴ ∠1=∠2,
∴ AD平分∠BAC;
(2)由(1)知 △ABD≌△ACD,
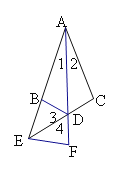
∴ ∠ADB=∠ADC,∠1=∠2,
在△ACE中,∠C=100°,∠BAC=40°,
∴∠1=∠2 =20°,
∴ ∠ADB=∠ADC=180°- ∠2 -∠C = 60°,
∴∠3=180°- ∠ADB-∠ADC=60°,
∵∠4=∠ADC=60°,
又DF=DC,DB=DC,
∴DB=DF,
在△BED和△EFD中,
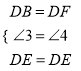 ,
,
∴△BED≌△EFD(SAS).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某省有7万名学生参加初中毕业会考,要想了解7万名学生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这1000名考生是总体的一个样本B.本调查是全面调查
C.7万名考生是总体D.每位考生的数学成绩是个体
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各变形中,不正确的是( )
A. 从x+3=6,可得x=6﹣3
B. 从2x=x﹣2,可得2x﹣x=﹣2
C. 从x+1=2x,可得x﹣2x=1
D. 从2x﹣4=3x+8,可得2x﹣3x=8+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
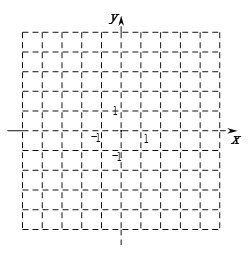
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
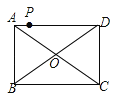
A.4.8 B.5 C.6 D.7.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com