
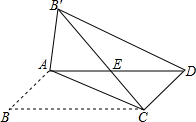
 如图,在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′C,B′D,B′C交AD于点E.
如图,在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′C,B′D,B′C交AD于点E.分析 (1)首先根据平行四边形的性质可证出∠DAC=∠ACB,根据翻折可得∠ACB′=∠ACB,进而可得∠DAC=∠ACB′,从而可得AE=CE,再证明B′E=DE,可得∠CB′D=∠ADB′,从而可得∠ADB′=∠DAC,进而可得B′D∥AC;
(2)作AF⊥BC于F,作CG⊥AD于G,根据三角函数值可得AF=BF=1,CG=DG=1,然后可得AG=2,设AE=CE=x,则EG=2-x,利用勾股定理可计算出x的值,然后计算△AEC的面积.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB,
∵将△ABC沿AC翻折至△AB′C,
∴∠ACB′=∠ACB,
∴∠DAC=∠ACB′,
∴AE=CE,
∵四边形ABCD是平行四边形,
∴AD=BC,
∵将△ABC沿AC翻折至△AB′C,
∵B′C=BC,
∴B′C=AD,
∴B′E=DE,
∴∠CB′D=∠ADB′,
∵∠AEC=∠B′ED,∠ACB′=∠CAD,
∴∠ADB′=∠DAC,
∴B′D∥AC;
(2)作AF⊥BC于F,作CG⊥AD于G,
∵∠B=45°,AB=$\sqrt{2}$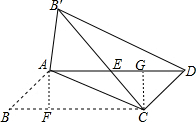 ,
,
∴AF=BF=1,CG=DG=1,
∵BC=3,
∴AG=2,
设AE=CE=x,则EG=2-x,
∵CG2+EG2=CE2,
∴12+(2-x)2=x2,解得x=$\frac{5}{4}$,
∴AE=$\frac{5}{4}$,
∴△AEC的面积=$\frac{1}{2}$AE•CG=$\frac{1}{2}$×$\frac{5}{4}$×1=$\frac{5}{8}$,
点评 此题主要考查了平行四边形的性质,勾股定理的应用,关键是掌握平行四边形对边平行且相等.


科目:初中数学 来源: 题型:解答题
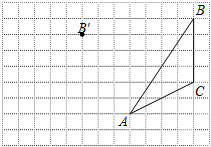 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 缩小为原来的$\frac{1}{5}$ | D. | 扩大为原来的10倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解在校大学生的主要娱乐方式 | |
| B. | 了解“嫦娥三号”卫星零部件的状况 | |
| C. | 日光灯管厂要检测一批灯管的使用寿命 | |
| D. | 了解某市居民对废电池的处理情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )
如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )| A. | $\frac{1}{{{2^{2013}}}}$ | B. | $\frac{1}{{{2^{2014}}}}$ | C. | $\frac{1}{{{2^{2015}}}}$ | D. | $\frac{1}{{{2^{2016}}}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com