
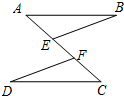
 如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF.
如图,点E,F在线段AC上,AB∥CD,AB=CD,AE=CF.求证:BE=DF. 科目:初中数学 来源: 题型:解答题
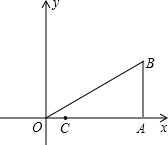 在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=3,以O为原点,OA所在的直线为x轴,建立如图所示的直角坐标系,点C的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,当PA+PC取最小值时.
在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=3,以O为原点,OA所在的直线为x轴,建立如图所示的直角坐标系,点C的坐标为($\frac{1}{2}$,0),点P为斜边OB上的一个动点,当PA+PC取最小值时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
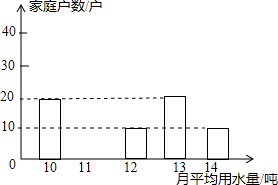 为了倡导“节约用水,从我做起”,某市政府决定对市直机关500户家庭的用水情况作一次调查.市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,某市政府决定对市直机关500户家庭的用水情况作一次调查.市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
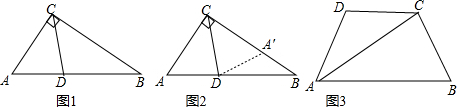
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
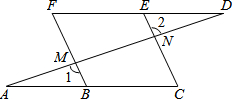 如图,已知,∠1=∠2,∠A=∠D,对∠C=∠F说明理由.
如图,已知,∠1=∠2,∠A=∠D,对∠C=∠F说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
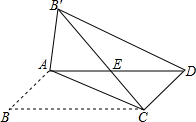 如图,在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′C,B′D,B′C交AD于点E.
如图,在?ABCD中,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′C,B′D,B′C交AD于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com