
【题目】由于受到手机更新换代的影响,某手机店经销![]() 型号手机四月售价比三月每台降价500元.如果卖出相同数量的
型号手机四月售价比三月每台降价500元.如果卖出相同数量的![]() 型号手机,那么三月销售额为9万元,四月销售额只有8万元.
型号手机,那么三月销售额为9万元,四月销售额只有8万元.
(1)三月![]() 型号手机每台售价为多少元?
型号手机每台售价为多少元?
(2)为了提高利润,该店计划五月购进![]() 型号手机销售,已知
型号手机销售,已知![]() 型号每台进价为3500元,
型号每台进价为3500元,![]() 型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)该店计划六月对![]() 型号的尾货进行销售,决定在四月售价基础上每售出一台
型号的尾货进行销售,决定在四月售价基础上每售出一台![]() 型号手机再返还顾客现金
型号手机再返还顾客现金![]() 元,而
元,而![]() 型号按销售价4400元销售,如要使(2)中所有方案获利相同,
型号按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
【答案】(1)4500;(2)共有5种进货方案;(3)当![]() 时,(2)中所有的方案获利相同.
时,(2)中所有的方案获利相同.
【解析】
(1)设三月份![]() 型号手机每台售价为x元,则四月份
型号手机每台售价为x元,则四月份![]() 型号手机每台售价为(x-500)元,根据三月份与四月份手机的销量相等建立方程求出其解件即可;
型号手机每台售价为(x-500)元,根据三月份与四月份手机的销量相等建立方程求出其解件即可;
(2)设购进![]() 型号手机m台,则
型号手机m台,则![]() 型号购进(20-m)台,根据两款手机的总费用不多于7.6万元且不少于7.4万元建立不等式组求出其解即可;
型号购进(20-m)台,根据两款手机的总费用不多于7.6万元且不少于7.4万元建立不等式组求出其解即可;
(3)根据两款手机的费用之和建立解析式,由解析式的性质就可以求出结论.
(1)设三月![]() 型号手机每台售价为
型号手机每台售价为![]() 元,由题意得:
元,由题意得:
![]()
解得![]()
经检验![]() 是方程的解.
是方程的解.
答:三月![]() 型号手机每台售价为4500元.
型号手机每台售价为4500元.
(2)设购进![]() 型号手机
型号手机![]() 台,由题意得:
台,由题意得:![]() ,解得:
,解得:![]()
![]() 只能取整数,
只能取整数,![]() 取8、9、10、11、12,共有5种进货方案.
取8、9、10、11、12,共有5种进货方案.
(3)四月![]() 型号手机每台售价是:
型号手机每台售价是:![]() (元),则总获利为
(元),则总获利为![]()
要使(2)中所有方案获利相同,则必须![]() ,解得:
,解得:![]()
答:当![]() 时,(2)中所有的方案获利相同.
时,(2)中所有的方案获利相同.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=BD;③PE2+PF2=PO2.其中正确的有( )

A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“小口罩,大温暖”为有效防控疫情,缓解基层防疫物资短缺问题,2020年2月10日,福山区首批4万只口罩免费派发.烟台市政府紧急调拨的这批民用口罩包括A,B两种不同款型,其中A型口罩单价80元/盒,B型口罩单价100元/盒.
(1)先进行试点发放,某社区环卫工人共收到A、B两种款型的口罩100盒,总价值共计9200元.求免费发放给该社区环卫工人的A型口罩和B型口罩各多少盒?
(2)我区某街道办事处决定将此项公益活动在其整个街道社区全面铺开.此公益活动得到部分厂家支持,某口罩制造厂对此批口罩进行打折销售,具体如下:A型口罩按原价的八折销售,B型口罩超出5盒的的部分按原价的六折销售.分别写出购买两种口罩费用y关于购买数量x(x>5)的函数关系式;并求购买多少盒口罩时,两种型号口罩花费同样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
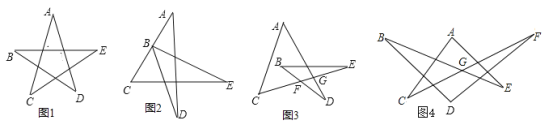
【题目】直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
(问题探究)
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E= ;
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
(变式拓展)
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
【1】如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .
【1】在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
【1】如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD=![]() ,求BC的长.
,求BC的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为4.

(1)数 所表示的点是(M,N)的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有1个白球、3个红球和6个黄球,这些球除颜色外都相同,将球摇匀.
(1) 从中任意摸出1个球,摸到 球的可能性大.
(2) 若现拿红球和黄球共7个球放入袋中,你认为怎样放才能让摸到红球和黄球的可能性相同?(直接回答,无需解题过程)
(3) 若从中摸出5个球,其中有![]() 个黄球,当
个黄球,当![]() = 时,“摸到白球”是必然事件?
= 时,“摸到白球”是必然事件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与坐标轴分别交于A、B点,AE平分
的图象与坐标轴分别交于A、B点,AE平分![]() ,交
,交![]() 轴于点E.
轴于点E.

(1)直接写出点A和点B的坐标.
(2)求直线AE的表达式.
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com