
【题目】直线在同一平面内有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同关系,今天我们就来探究一下这些奇妙的图形吧!
(问题探究)
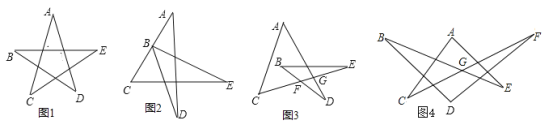
(1)如图1,请直接写出∠A+∠B+∠C+∠D+∠E= ;
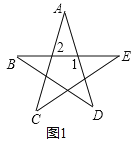
(2)将图1变形为图2,∠A+∠DBE+∠C+∠D+∠E的结果如何?请写出证明过程;
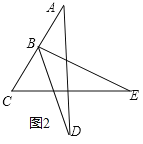
(3)将图1变形为图3,则∠A+∠B+∠C+∠D+∠E的结果如何?请写出证明过程.
(变式拓展)
(4)将图3变形为图4,已知∠BGF=160°,那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
【答案】(1)![]() ;(2)
;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]()
![]() ;证明见解析;(4)
;证明见解析;(4)![]() .
.
【解析】
(1)根据三角形外角的性质∠2=∠C+∠E,∠1=∠A+∠2,根据三角形内角和等于180°即可求解.
(2)根据三角形外角的性质∠ABE=∠C+∠E,∠DBC=∠A+∠D,即可证明此结论.
(3)根据三角形外角的性质,∠DFG=∠B+∠E,∠FGD=∠A+∠C,即可证明此结论.
(4)根据三角形内角和定理和三角形的性质进行转换即可得出答案.
(1)如图1,
∵∠2=∠C+∠E,∠1=∠A+∠2,
∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°;
故答案为:180°;
(2)将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°.
证明:如图2,
∵∠ABE=∠C+∠E,∠DBC=∠A+∠D,
∠ABE+∠DBE+∠DBC=180°,
∴∠A+∠DBE+∠C+∠D+∠E=180°
![]()
∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°;
(3)将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°.
证明:如图3,
∵在△FGD中,∠DFG+∠FGD+∠D=180°,
∠DFG=∠B+∠E,∠FGD=∠A+∠C,
∴∠A+∠B+∠C+∠D+∠E=180°,
∴将图①变形成图③,则∠A+∠B+∠C+∠D+∠E还为180°.
(4)320°.
如图4,
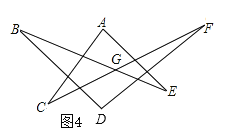
根据三角形中,一个内角的补角等于其余两个内角的和,
∴四边形FGBD中:∠FGB=∠B+∠D+∠F,
四边形ACGE中:∠CGE=∠A+∠C+∠E,
∵∠CGE=∠BGF=160°,
∴∠A+∠B+∠C+∠D+∠E+∠F=320°,
故答案为:320°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:对于任意正实数a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在![]() ≥
≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
根据上述内容,填空:若m>0,只有当m= 时,![]() 有最小值,最小值为 .
有最小值,最小值为 .
探索应用:如图,已知![]() ,
,![]() ,
,![]() 为双曲线
为双曲线![]() (x>0)上的任意一点,过点
(x>0)上的任意一点,过点![]() 作
作![]() ⊥x轴于点
⊥x轴于点![]() ,
,![]() ⊥y轴于点D.求四边形
⊥y轴于点D.求四边形![]() 面积的最小值,并说明此时四边形
面积的最小值,并说明此时四边形![]() 的形状.
的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB,BC.
求作:平行四边形ABCD.
以下是甲、乙两同学的作业.
甲:
①以点C为圆心,AB长为半径作弧;
②以点A为圆心,BC长为半径作弧;
③两弧在BC上方交于点D,连接AD,CD.
四边形ABCD即为所求平行四边形.(如图1)
乙:
①连接AC,作线段AC的垂直平分线,交AC于点M;
②连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD.
四边形ABCD即为所求平行四边形.(如图2)
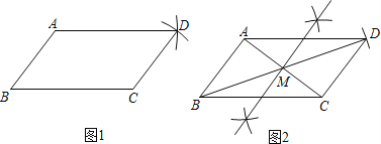
老师说甲、乙同学的作图都正确,你更喜欢______的作法,他的作图依据是:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线![]() 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象.
(2)点Q(8,m)在抛物线![]() 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销![]() 型号手机四月售价比三月每台降价500元.如果卖出相同数量的
型号手机四月售价比三月每台降价500元.如果卖出相同数量的![]() 型号手机,那么三月销售额为9万元,四月销售额只有8万元.
型号手机,那么三月销售额为9万元,四月销售额只有8万元.
(1)三月![]() 型号手机每台售价为多少元?
型号手机每台售价为多少元?
(2)为了提高利润,该店计划五月购进![]() 型号手机销售,已知
型号手机销售,已知![]() 型号每台进价为3500元,
型号每台进价为3500元,![]() 型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)该店计划六月对![]() 型号的尾货进行销售,决定在四月售价基础上每售出一台
型号的尾货进行销售,决定在四月售价基础上每售出一台![]() 型号手机再返还顾客现金
型号手机再返还顾客现金![]() 元,而
元,而![]() 型号按销售价4400元销售,如要使(2)中所有方案获利相同,
型号按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动;设该机器人每秒钟前进或后退1步,并且每步的距离是1个单位长,xn表示第n秒时机器人在数轴上的位置所对应的数;给出下列结论:(1)x3=3;(2)x5=1;(3)x108<x104;其中,正确结论的序号是( )
A. (1)、(3)B. (2)、(3)C. (1)、(2)D. (1)、(2)、(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠BAC=32°,斜边AC=6,将斜边AC绕点A逆时针方向旋转26°到达AD的位置,连接CD,取线段CD的中点N,连接BN,则BN的长为_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com