【题目】已知：线段AB，BC．
求作：平行四边形ABCD．
以下是甲、乙两同学的作业．
甲：
①以点C为圆心，AB长为半径作弧；
②以点A为圆心，BC长为半径作弧；
③两弧在BC上方交于点D，连接AD，CD．
四边形ABCD即为所求平行四边形．（如图1）
乙：
①连接AC，作线段AC的垂直平分线，交AC于点M；
②连接BM并延长，在延长线上取一点D，使MD=MB，连接AD，CD．
四边形ABCD即为所求平行四边形．（如图2）
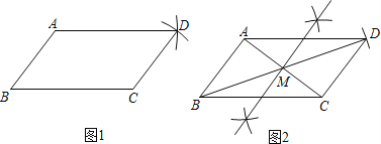
老师说甲、乙同学的作图都正确，你更喜欢______的作法，他的作图依据是：______．
科目：初中数学 来源： 题型：
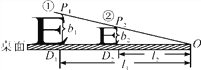
【题目】如图所示，在水平桌面上的两个“E”，当点P1，P2，O在一条直线上时，在点O处用①号“E”测得的视力与用②号“E”测得的视力相同．
(1)图中b1，b2，l1，l2满足怎样的关系式？
(2)若b1＝3.2 cm，b2＝2 cm，①号“E”的测量距离l1＝8 cm，要使测得的视力相同，则②号“E”的测量距离l2应为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线y＝
x与双曲线y＝
(k>0)交于A，B两点，且点A的横坐标为4.点C是双曲线上一点，且纵坐标为8，则△AOC的面积为( )
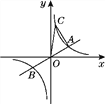
A. 8 B. 32 C. 10 D. 15
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作ABDE，连接AD，EC．
（1）求证：△ADC≌△ECD；
（2）若BD=CD，求证：四边形ADCE是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
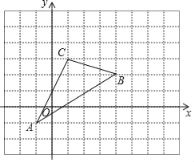
【题目】如图，三角形ABC在直角坐标系中．
（1）请直接写出点A、C两点的坐标：
（2）三角形ABC的面积是 ；
（3）若把三角形ABC向上平移1个单位，再向右平移1个单位得三角形A′B′C′在图中画出三角形A′B′C’，这时点B′的坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.“穿十条马路连遇十次红灯”是不可能事件
B.任意画一个三角形，其内角和是180°是必然事件
C.某彩票中奖概率为1%，那么买100张彩票一定会中奖
D.“福山福地福人居”这句话中任选一个汉字，这个字是“福”字的概率是
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】直线在同一平面内有平行和相交两种位置关系，线段首尾连接可以变换出很多不同的图形，这些不同的角又有很多不同关系，今天我们就来探究一下这些奇妙的图形吧！
（问题探究）
（1）如图1，请直接写出∠A+∠B+∠C+∠D+∠E= ；
（2）将图1变形为图2，∠A+∠DBE+∠C+∠D+∠E的结果如何？请写出证明过程；
（3）将图1变形为图3，则∠A+∠B+∠C+∠D+∠E的结果如何？请写出证明过程．
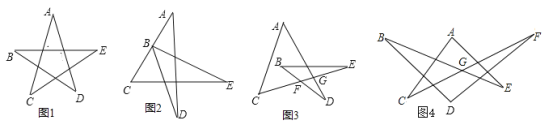
（变式拓展）
（4）将图3变形为图4，已知∠BGF=160°，那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，一次函数
(
为常数)的图象与反比例函数
(
为常数，且<0)的图象交于A，B两点．
(1) 如图①，当
，
时，
① A ( ， )，B ( ， )；
②直接写出使
成立的
的取值范围；
(2) 如图②，将(1)中直线AB向下平移，交反比例函数图像于点C，D，连接OC，AC，若△AOC的面积为8，求的值；
(3) 若A，B两点的横坐标分别为
，
，且，满足
，证明：2m-b=-3．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
