【题目】下列说法正确的是（ ）
A.“穿十条马路连遇十次红灯”是不可能事件
B.任意画一个三角形，其内角和是180°是必然事件
C.某彩票中奖概率为1%，那么买100张彩票一定会中奖
D.“福山福地福人居”这句话中任选一个汉字，这个字是“福”字的概率是
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，
，
的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，
，垂足为G，若
，则AE的边长为
A. 
B. 
C. 4 D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：线段AB，BC．
求作：平行四边形ABCD．
以下是甲、乙两同学的作业．
甲：
①以点C为圆心，AB长为半径作弧；
②以点A为圆心，BC长为半径作弧；
③两弧在BC上方交于点D，连接AD，CD．
四边形ABCD即为所求平行四边形．（如图1）
乙：
①连接AC，作线段AC的垂直平分线，交AC于点M；
②连接BM并延长，在延长线上取一点D，使MD=MB，连接AD，CD．
四边形ABCD即为所求平行四边形．（如图2）
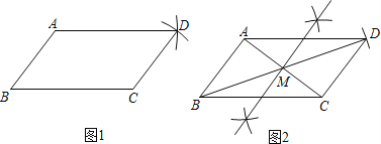
老师说甲、乙同学的作图都正确，你更喜欢______的作法，他的作图依据是：______．
查看答案和解析>>
科目：初中数学 来源： 题型：
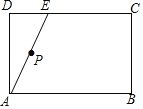
【题目】如图，矩形ABCD中，点E为矩形的边CD上的任意一点，点P为线段AE的中点，连接BP并延长与边AD交于点F，点M为边CD上的一点，且CM＝DE，连接FM．
（1）依题意补全图形；
（2）求证∠DMF＝∠ABF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于任意有理数a，b，定义运算：a⊙b＝a（a+b）﹣1，等式右边是通常的加法、减法、乘法运算，例如，2⊙5＝2×（2+5）﹣1＝13；（﹣3）⊙（﹣5）＝﹣3×（﹣3﹣5）﹣1＝23．
（1）求（﹣2）⊙3
的值；
（2）对于任意有理数m，n，请你重新定义一种运算“⊕”，使得5⊕3＝20，写出你定义的运算：m⊕n＝ （用含m，n的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点M（4，0），以点M为圆心、2为半径的圆与x轴交于点A、B．已知抛物线
过点A和B，与y轴交于点C．
（1）求点C的坐标，并画出抛物线的大致图象．
（2）点Q（8，m）在抛物线
上，点P为此抛物线对称轴上一个动点，求PQ＋PB的最小值．
（3）CE是过点C的⊙M的切线，点E是切点，求OE所在直线的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个机器人从数轴原点出发，沿数轴正方向，以每前进3步后退2步的程序运动；设该机器人每秒钟前进或后退1步，并且每步的距离是1个单位长，xn表示第n秒时机器人在数轴上的位置所对应的数；给出下列结论：（1）x3=3；（2）x5=1；（3）x108＜x104；其中，正确结论的序号是（ ）
A. （1）、（3）B. （2）、（3）C. （1）、（2）D. （1）、（2）、（3）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A（m，m＋1），B（m＋1，2m－3）都在反比例函数
的图象上．
（1）求m，k的值；
（2）如果M为x轴上一点，N为y轴上一点， 以点A，B，M，N为顶点的四边形是平行四边形，试求直线MN的函数表达式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
