【题目】如图，点
为
的
边的中点，分别以
、
为斜边作
和
，且
，
．
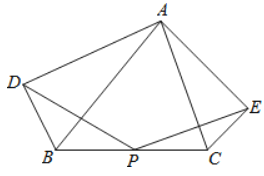
（1）求证：
．
（2）探究：
与
的数量关系，并证明你的结论．
【答案】（1）详见解析；（2）
，证明见解析．
【解析】
（1）如图，分别取
、
的中点
、
，连接
、
、
、
，根据三角形的中位线定理和直角三角形的性质可得
，
，根据等腰三角形的性质、三角形的外角性质和已知条件可得
，根据平行线的性质可得
=
，进而可得
，于是可根据SAS证明
，从而可得结论；
（2）根据平行线的性质可得
，根据全等三角形的性质可得
，然后在
中利用三角形的内角和定理和等量代换即可得出结论．
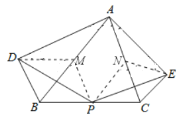
（1）证明：如图，分别取、的中点、，连接、、、．
点
为
的边
的中点，
∴
，
为
斜边上的中线，
∴
，
，
同理可得：，
，
，
，
同理，
，
又
，
，
又、都是的中位线，
，
，
，
，
，
∴，
，
；
（2）解：
与
的数量关系是：；
证明：
，
，
∵，
，
在中，∵
，
∴
，
而
，
，
，
．
科目：初中数学 来源： 题型：
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，把超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值（单位：克） | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）若每袋食品的标准质量为450克，则抽样检测的20袋食品的总质量是多少克？
（2）若该种食品的合格标准为450±5克，求该种食品抽样检测的合格率？
查看答案和解析>>
科目：初中数学 来源： 题型：
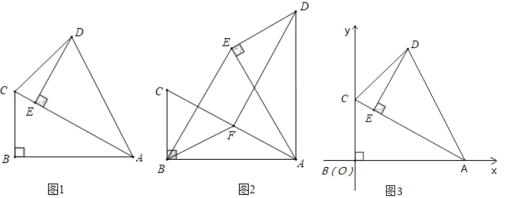
【题目】在
中，∠ABC=90°，∠BAC=30°，将
绕点A顺时针旋转一定的角度α得到
，点B、C的对应点分别是E、D．
（1）如图1，当点E恰好在AC上时，求∠CDE的度数；
（2）如图2，若α=60°时，点F是边AC中点，求证：DF=BE；
（3）如图3，点B、C的坐标分别是(0,0)，(0,2)，点Q是线段AC上的一个动点，点M是线段AO上的一个动点，是否存在这样的点Q、M使得
为等腰三角形且
为直角三角形？若存在，请直接写出满足条件的点M的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
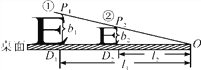
【题目】如图所示，在水平桌面上的两个“E”，当点P1，P2，O在一条直线上时，在点O处用①号“E”测得的视力与用②号“E”测得的视力相同．
(1)图中b1，b2，l1，l2满足怎样的关系式？
(2)若b1＝3.2 cm，b2＝2 cm，①号“E”的测量距离l1＝8 cm，要使测得的视力相同，则②号“E”的测量距离l2应为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
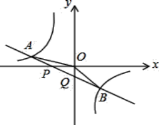
【题目】如图，已知直线y=k1x+b与x轴、y轴相交于P，Q两点，与y=
的图象相交于A（－2，m），B（1，n）两点，连接OA，OB，给出下列论：①k1k2<0；②m+
n=0；③S△AOP=S△BOQ；④不等式k1x+b>的解集为x<－2或0<x<1．其中正确的结论是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度，则点B所对应的数是_____.
(2)在(1)的条件下，点A以每秒2个单位长度沿数轴向左运动，点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时，求A、B两点间的距离.
(3)在(2)的条件下，现A点静止不动，B点以原速沿数轴向左运动，经过多长时间A、B两点相距4个单位长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
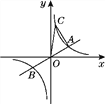
【题目】如图，已知直线y＝
x与双曲线y＝
(k>0)交于A，B两点，且点A的横坐标为4.点C是双曲线上一点，且纵坐标为8，则△AOC的面积为( )
A. 8 B. 32 C. 10 D. 15
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.“穿十条马路连遇十次红灯”是不可能事件
B.任意画一个三角形，其内角和是180°是必然事件
C.某彩票中奖概率为1%，那么买100张彩票一定会中奖
D.“福山福地福人居”这句话中任选一个汉字，这个字是“福”字的概率是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
