
【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P,Q两点,与y=![]() 的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列论:①k1k2<0;②m+
的图象相交于A(-2,m),B(1,n)两点,连接OA,OB,给出下列论:①k1k2<0;②m+![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b>
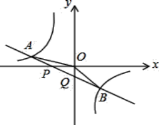
n=0;③S△AOP=S△BOQ;④不等式k1x+b>![]() 的解集为x<-2或0<x<1.其中正确的结论是________.
的解集为x<-2或0<x<1.其中正确的结论是________.
【答案】②③④
【解析】
根据一次函数和反比例函数的性质得到k1k2>0,故①错误;把A(-2,m)、B(1,n)代入y=![]() 中得到-2m=n故②正确;把A(-2,m)、B(1,n)代入y=k1x+b得到y=-mx-m,求得P(-1,0),Q(0,-m),根据三角形的面积公式即可得到S△AOP=S△BOQ;故③正确;根据图象得到不等式k1x+b>
中得到-2m=n故②正确;把A(-2,m)、B(1,n)代入y=k1x+b得到y=-mx-m,求得P(-1,0),Q(0,-m),根据三角形的面积公式即可得到S△AOP=S△BOQ;故③正确;根据图象得到不等式k1x+b>![]() 的解集是x<-2或0<x<1,故④正确.
的解集是x<-2或0<x<1,故④正确.
:由图象知,k1<0,k2<0,
∴k1k2>0,故①错误;
把A(-2,m)、B(1,n)代入y=![]() 中得-2m=n,
中得-2m=n,
∴m+![]() n=0,故②正确;
n=0,故②正确;
把A(-2,m)、B(1,n)代入y=k1x+b得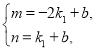
∴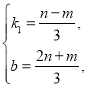 ,
,
∵-2m=n,
∴y=-mx-m,
∵已知直线y=k1x+b与x轴、y轴相交于P、Q两点,
∴P(-1,0),Q(0,-m),
∴OP=1,OQ=m,
∴S△AOP=![]() m,S△BOQ=
m,S△BOQ=![]() m,
m,
∴S△AOP=S△BOQ;故③正确;
由图象知不等式k1x+b>![]() 的解集是x<-2或0<x<1,故④正确;
的解集是x<-2或0<x<1,故④正确;
故答案为:②③④.


科目:初中数学 来源: 题型:
【题目】(1)如图,已知直线AB、CD交于点O,OE平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.

(2)计算题
①![]() -
-![]() +
+![]() -
-![]() ②4(x﹣2)2-25=0
②4(x﹣2)2-25=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
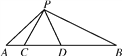
【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式.例如:![]() .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像![]() ,
,![]() ,…这样的分式是假分式;像
,…这样的分式是假分式;像![]() ,
,![]() ,…这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式. 例如:
,…这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式. 例如: ![]() ’
’
![]() .
.
(1)将分式![]() 化为整式与真分式的和的形式;
化为整式与真分式的和的形式;
(2)如果分式![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于任意正实数a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在![]() ≥
≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
根据上述内容,填空:若m>0,只有当m= 时,![]() 有最小值,最小值为 .
有最小值,最小值为 .
探索应用:如图,已知![]() ,
,![]() ,
,![]() 为双曲线
为双曲线![]() (x>0)上的任意一点,过点
(x>0)上的任意一点,过点![]() 作
作![]() ⊥x轴于点
⊥x轴于点![]() ,
,![]() ⊥y轴于点D.求四边形
⊥y轴于点D.求四边形![]() 面积的最小值,并说明此时四边形
面积的最小值,并说明此时四边形![]() 的形状.
的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习绝对值后,我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离.而|5|=|5﹣0|,即|5﹣0|也可理解为5、0在数轴上对应的两点之间的距离.类似的,|5-3|表示5与3之差的绝对值,也可理解为5与3两数在数轴上所对应的两点之间的距离.如|x-3|的几何意义是数轴上表示有理数3的点与表示数x的点之间的距离,一般地,点A、B在数轴上分别表示数a、b,那么A、B之间的距离可表示为|a﹣b|.
请根据绝对值的意义并结合数轴解答下列问题:
![]()
(1)数轴上表示2和3的两点之间的距离是 ;数轴上表示数a的点与表示﹣2的点之间的距离表示为 ;
(2)数轴上点P表示的数是2,P、Q两点的距离为3,则点Q表示的数是 ;
(3)数轴上有一个点表示数a,则|a+1|+|a-3|+|a+8|的最小值为 ;
(4)a、b、c、d在数轴上的位置如下图所示,若|a-d|=12,|b-d|=7,|a-c|=9,则|b-c|等于 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com