【题目】(1)如图，已知直线AB、CD交于点O，OE平分∠BOD，若∠3：∠2=8：1，求∠AOC的度数．
(2)计算题
①
－
＋
－
②4（x﹣2）2-25=0
【答案】（1）36°；（2）①1；②
【解析】
（1）根据角平分线的定义得∠1=∠2，由∠3：∠2=8：1得∠3=8∠2．根据平角的定义有∠1+∠2+∠3=180°，则∠2+∠2+8∠2=180°，可解得出∠2=18°，而根据对顶角相等有∠AOC=∠1+∠2，然后把∠1、∠2的度数代入计算即可．
(2)
（1）根据开方运算，可化简根式，根据实数的运算，可得答案．
（2）解方程，先等式移向，开根号分别求得x的值即可.
（1）∵平分∠BOD，
∴∠1=∠2，
∵∠3:∠2=8:1，
∴∠3=8∠2.
∵∠1+∠2+∠3=180°，
∴∠2+∠2+8∠2=180°，
解得∠2=18°，
∴∠AOC=∠1+∠2=36°.
故答案为：36°
（2）①
－
＋
－
=
=
=1
②∵4（x﹣2）2-25=0
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案科目：初中数学 来源： 题型：
【题目】把下列各数：
﹣3.1，3.1415，﹣
，+31，0.618，﹣
，0，﹣1，﹣（﹣3），填在相应的集合里
分数集合： ；
整数集合： ；
非负整数集合： ；
正有理数集合： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，有一个可以自由转动的转盘被平均分成3个扇形，分别标有1、2、3三个数字，小王和小李各转动一次转盘为一次游戏，当每次转盘停止后，指针所指扇形内的数为各自所得的数，一次游戏结束得到一组数（若指针指在分界线时重转）．
（1）请你用树状图或列表的方法表示出每次游戏可能出现的所有结果；
（2）求每次游戏结束得到的一组数恰好是方程x2-3x+2=0的解的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，把超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值（单位：克） | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）若每袋食品的标准质量为450克，则抽样检测的20袋食品的总质量是多少克？
（2）若该种食品的合格标准为450±5克，求该种食品抽样检测的合格率？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在平面直角坐标系中，点A（0，4），点B（m，0），以AB为边在右侧作正方形ABCD．
（1）当点B在x轴正半轴上运动时，求点C点的坐标．（用m表示）
（2）当m=0时，如图2，P为OA上一点，过点P作PM⊥PC，PM=PC，连MC交OD于点N，求AM+2DN的值；
（3）如图3，在第（2）问的条件下，E、F分别为CD、CO上的点，作EG∥x轴交AO于G，作FH∥y轴交AD于H，K是EG与FH的交点．若S四边形KFCE=2S四边形AGKH，试确定∠EAF的大小，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为保护环境，我市某公交公司计划购买A型和B型两种环保节能公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车3辆，B型公交车2辆，共需600万元．
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案?
(3)在(2)的条件下，哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
科目：初中数学 来源： 题型：
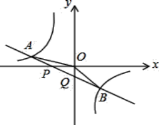
【题目】如图，已知直线y=k1x+b与x轴、y轴相交于P，Q两点，与y=
的图象相交于A（－2，m），B（1，n）两点，连接OA，OB，给出下列论：①k1k2<0；②m+
n=0；③S△AOP=S△BOQ；④不等式k1x+b>的解集为x<－2或0<x<1．其中正确的结论是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
