
����Ŀ��Ϊ��������������ij������˾�ƻ�����A�ͺ�B�����ֻ������ܹ�������10����������A������1����B������2��������400��Ԫ��������A������3����B������2��������600��Ԫ��
(1)����A�ͺ�B������ÿ�����������Ԫ?
(2)Ԥ����ij��·��A�ͺ�B������ÿ������ؿ����ֱ�Ϊ60���˴κ�100���˴Σ����ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ��ܺͲ�����680���˴Σ���ù�˾���ļ��ֹ�������?
(3)��(2)�������£����ֹ��������ܷ�������?�����ܷ����Ƕ�����Ԫ?
���𰸡���1��A��100��Ԫ��B��150��Ԫ����2�����ַ�����A��6����B��4����A��7����B��3����A��8����B��2������3��A��8����B��2�����������٣����ٷ���Ϊ1100��Ԫ
��������
��1�����ݡ�����A������1����B������2��������400��Ԫ������A������3����B������2��������600��Ԫ��, �ֱ��蹺��A������ÿ����x��Ԫ, ����B������ÿ����y��Ԫ, �ж�Ԫһ�η�����![]() ��⼴�ɣ�
��⼴�ɣ�
��2���蹺��A������a��, ��B������(10- a)��, �г�����ʽ�� �����a��ȡֵ��Χ6��a��8����ˣ�����������A��������a��Ϊ6��7��8�������Ӧ��B��������Ϊ4��3��2������һ�������ַ�����
�����a��ȡֵ��Χ6��a��8����ˣ�����������A��������a��Ϊ6��7��8�������Ӧ��B��������Ϊ4��3��2������һ�������ַ�����
��3���ڣ�2����������ַ����Ļ����ϣ��ֱ���и����������ܷ��ü��㣬ͨ���Ƚϣ����ɵó�����A������8��, ��B������2���ܷ������٣�����Ϊ1100��Ԫ.
�⣺ (1)�蹺��A������ÿ����x��Ԫ, ����B������ÿ����y��Ԫ,�������:
![]()
���![]()
��:����A������ÿ����100��Ԫ, ����B������ÿ����150��Ԫ.
(2)�蹺��A������a��, ��B������(10- a)��, �������

���: 6��a��8,
��a=6,7, 8 ;
��(10-a) =4,3,2;
���ַ���: ��������
�ٹ���A������6��, ��B������4��;
�ڹ���A������7��, ��B������3��;
�۹���A������8��, ��B������2��;
(3)�ٹ���A������6��, ��B������4��:
100��6+150��4= 1200��Ԫ;
�ڹ���A������7��, ��B������3��:
100��7+150��3=1150��Ԫ;
�۹���A������8��, ��B������2��:
100��8+150�� 2= 1100��Ԫ;
�ʹ���A������8��,��B������2����������, �����ܷ���Ϊ1100��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ȱ�![]() �Ķ���
�Ķ���![]() ��
��![]() ��ĸ������ϣ���
��ĸ������ϣ���![]() ������Ϊ
������Ϊ![]() �����
�����![]() ����Ϊ_______����
����Ϊ_______����![]() ��λ��
��λ��![]() ���ϵ�
���ϵ�![]() ��ߵ�һ�����㣬��
��ߵ�һ�����㣬��![]() Ϊ���ڵ������������ȱ�
Ϊ���ڵ������������ȱ�![]() ,����
,����![]()
![]() .С�����ڵ���ѧ��Ȥ����ѧϰС��������ִ���������Ϣ����������ʱ�侭��̽���������۵�
.С�����ڵ���ѧ��Ȥ����ѧϰС��������ִ���������Ϣ����������ʱ�侭��̽���������۵�![]() �ڵ�
�ڵ�![]() ���
���![]() �Ḻ�����κ�λ�ã�
�Ḻ�����κ�λ�ã�![]() ��
��![]() ֮�䶼������һ���̶���һ�κ�����ϵ������д�������ϵʽ��_____��
֮�䶼������һ���̶���һ�κ�����ϵ������д�������ϵʽ��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ����ֱ֪��AB��CD���ڵ�O��OEƽ�֡�BOD������3����2=8��1�����AOC�Ķ�����

(2)������
��![]() ��
��![]() ��
��![]() ��
��![]() ��4��x��2��2-25=0
��4��x��2��2-25=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�CD=6����E�ڱ�CD�ϣ���CD=3DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF��

��1����֤���١�ABG�ա�AFG�� ����GC�ij���
��2������FGC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��������ͬʱ�����330ǧ�ļס�������������У�s��ǧ�ף���ʾ������صľ��룬t���֣���ʾ������ʻ��ʱ�䣬��ͼ��L1��L2�ֱ��ʾ����������s��t�Ĺ�ϵ��
��1��L1��ʾ�����������صľ�������ʻʱ��Ĺ�ϵ��
��2������B���ٶ��Ƕ��٣�
��3����L1��L2�ֱ��ʾ������������s��t�Ĺ�ϵʽ��
��4��2Сʱ������������ǧ�ף�
��5����ʻ�ʱ���A��B����������
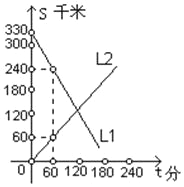
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�鳤���θְ壬����ʦ��������ֳ������ȵ������֣�������ͼ�л�����ͼ�ۼ���
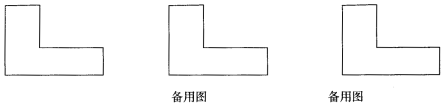
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ���ı���ֽƬABCD����B=��D=90�㣬��ֽƬ����ͼ��ʾ�۵���ʹ��B����AD���ϵ�B'�㣬AE���ۺۡ�

��1�����ж�B'E��DC��λ�ù�ϵ��˵�����ɡ�
��2�������C=130�㣬���AEB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��D���߶�AB�ϣ���PCD�ǵȱ������Σ�
(1)��AC��CD��DB���������Ĺ�ϵʱ����ACP�ס�PDB?
(2)����ACP�ס�PDBʱ�����APB�Ķ�����
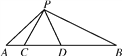
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ����ֵ������֪����|a|��ʾ��a�������ϵĶ�Ӧ����ԭ��ľ��룮�磺|5|��ʾ5�������ϵĶ�Ӧ�㵽ԭ��ľ��룮��|5|=|5��0|����|5��0|Ҳ������Ϊ5��0�������϶�Ӧ������֮��ľ��룮���Ƶģ�|5��3|��ʾ5��3֮��ľ���ֵ��Ҳ������Ϊ5��3����������������Ӧ������֮��ľ��룮��|x��3|�ļ��������������ϱ�ʾ������3�ĵ����ʾ��x�ĵ�֮��ľ���,һ��أ���A��B�������Ϸֱ��ʾ��a��b����ôA��B֮��ľ���ɱ�ʾΪ|a��b|��
����ݾ���ֵ�����岢����������������⣺
![]()
��1�������ϱ�ʾ2��3������֮��ľ����� �������ϱ�ʾ��a�ĵ����ʾ��2�ĵ�֮��ľ����ʾΪ ��
��2�������ϵ�P��ʾ������2��P��Q����ľ���Ϊ3�����Q��ʾ������ ��
��3����������һ�����ʾ��a����|a+1|+|a-3|+|a+8|����СֵΪ ��
��4��a��b��c��d�������ϵ�λ������ͼ��ʾ����|a-d|=12��|b-d|=7��|a-c|=9����|b-c|���� .
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com