
【题目】如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数![]() 的图象上.
的图象上.

(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
【答案】(1)m=3,k=12;(2)![]() 或
或![]()
【解析】
试题分析:(1)根据反比例函数图象上的点的坐标的特征可得![]() ,即可求得结果;
,即可求得结果;
(2)存在两种情况,①当M点在x轴的正半轴上,N点在y轴的正半轴上时,②当M点在x轴的负半轴上,N点在y轴的负半轴上时,根据平行四边形的性质求解即可.
(1)由题意可知,![]()
解得m1=3,m2=-1(舍去)
∴A(3,4),B(4,3);
∴k=4×3=12;
(2)存在两种情况,如图:
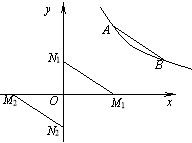
①当M点在x轴的正半轴上,N点在y轴的正半轴上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵四边形AN1M1B为平行四边形,
∴线段N1M1可看作由线段AB向左平移3个单位,再向下平移3个单位得到的
由(1)知A点坐标为(3,4),B点坐标为(4,3),
∴N1点坐标为(0,1),M1点坐标为(1,0)
设直线M1N1的函数表达式为![]() ,把x=1,y=0代入,解得
,把x=1,y=0代入,解得![]() .
.
∴直线M1N1的函数表达式为![]() ;
;
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴N1M1∥M2N2,N1M1=M2N2.
∴线段M2N2与线段N1M1关于原点O成中心对称.
∴M2点坐标为(-1,0),N2点坐标为(0,-1).
设直线M2N2的函数表达式为![]() ,把x=-1,y=0代入,解得
,把x=-1,y=0代入,解得![]() ,
,
∴直线M2N2的函数表达式为![]()
所以,直线MN的函数表达式为![]() 或
或![]() .
.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“穿十条马路连遇十次红灯”是不可能事件
B.任意画一个三角形,其内角和是180°是必然事件
C.某彩票中奖概率为1%,那么买100张彩票一定会中奖
D.“福山福地福人居”这句话中任选一个汉字,这个字是“福”字的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受气候的影响,某超市蔬菜供应紧张,需每天从外地调运蔬菜1000斤.超市决定从甲、乙两大型蔬菜棚调运蔬菜,已知甲蔬菜棚每天最多可调出800斤,乙蔬菜棚每天最多可调运600斤,从两蔬菜棚调运蔬菜到超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲蔬菜棚 | 120 | 0.03 |
乙蔬菜棚 | 80 | 0.05 |
(1)若某天调运蔬菜的总运费为3840元,则从甲、乙两蔬菜棚各调运了多少斤蔬菜?
(2)设从甲蔬菜棚调运蔬菜![]() 斤,总运费为
斤,总运费为![]() 元,试写出
元,试写出![]() 与
与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数![]() (
(![]() 为常数)的图象与反比例函数
为常数)的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() <0)的图象交于A,B两点.
<0)的图象交于A,B两点.
(1) 如图①,当![]() ,
,![]() 时,
时,
① A ( , ),B ( , );
②直接写出使![]() 成立的
成立的![]() 的取值范围;
的取值范围;
(2) 如图②,将(1)中直线AB向下平移,交反比例函数图像于点C,D,连接OC,AC,若△AOC的面积为8,求![]() 的值;
的值;
(3) 若A,B两点的横坐标分别为![]() ,
,![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,证明:2m-b=-3.
,证明:2m-b=-3.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.

∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=___(___),
∴AB∥EF(___)
∵∠3=___(___)
又∠B=∠3(已知)
∴∠B=___(等量代换)
∴DE∥BC(___)
∴∠C=∠AED(___).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象过点A(0,3)和点B(3,0),且与正比例函数
的图象过点A(0,3)和点B(3,0),且与正比例函数![]() 的图象交于点P.
的图象交于点P.
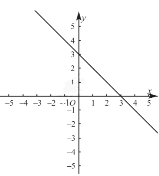
(1)求函数![]() 的解析式和点P的坐标.
的解析式和点P的坐标.
(2)画出两个函数 的图象,并直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
(3)若点Q是![]() 轴上一点,且△PQB的面积为8,求点Q的坐标.
轴上一点,且△PQB的面积为8,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.
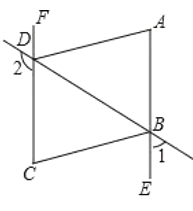
(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB=|a﹣b|,回答下列问题:
(1)数轴上表示1和﹣3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点分别是点A和B,如果AB=2,那么x= ;
(3)当|x﹣6|+|x﹣1|的最小值是 。若|x﹣3|+|x﹣b|的最小值为4,则b的值为 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com