
【题目】已知一次函数![]() 的图象过点A(0,3)和点B(3,0),且与正比例函数
的图象过点A(0,3)和点B(3,0),且与正比例函数![]() 的图象交于点P.
的图象交于点P.
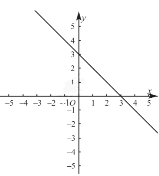
(1)求函数![]() 的解析式和点P的坐标.
的解析式和点P的坐标.
(2)画出两个函数 的图象,并直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
(3)若点Q是![]() 轴上一点,且△PQB的面积为8,求点Q的坐标.
轴上一点,且△PQB的面积为8,求点Q的坐标.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线![]() 过点A和B,与y轴交于点C.
过点A和B,与y轴交于点C.
(1)求点C的坐标,并画出抛物线的大致图象.
(2)点Q(8,m)在抛物线![]() 上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
上,点P为此抛物线对称轴上一个动点,求PQ+PB的最小值.
(3)CE是过点C的⊙M的切线,点E是切点,求OE所在直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线![]() 和矩形
和矩形![]() 构成,矩形的长
构成,矩形的长![]() 是
是![]() ,宽
,宽![]() 是
是![]() ,拱顶
,拱顶![]() 到地面
到地面![]() 的距离是
的距离是![]() ,若以
,若以![]() 原点,
原点, ![]() 所在的直线为
所在的直线为![]() 轴,
轴, ![]() 所在的直线为
所在的直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
(![]() )画出平面直角坐标系
)画出平面直角坐标系![]() ,并求出抛物线
,并求出抛物线![]() 的函数表达式.
的函数表达式.
(![]() )在抛物线型拱壁
)在抛物线型拱壁![]() ,
, ![]() 处安装两盏灯,它们离地面
处安装两盏灯,它们离地面![]() 的高度都是
的高度都是![]() ,则这两盏灯的水平距离
,则这两盏灯的水平距离![]() 是多少米?
是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,m+1),B(m+1,2m-3)都在反比例函数![]() 的图象上.
的图象上.

(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点, 以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的大括号里:
-6, 9.3,![]() ,42,0,-0.33,0.333…,1.41421356,-2π,3.3030030003…,-3.1415926.
,42,0,-0.33,0.333…,1.41421356,-2π,3.3030030003…,-3.1415926.
正数集合{ };
负数集合{ };
有理数集合{ };
无理数集合{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O.
(1)作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);
(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.
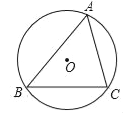
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com