练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，隧道的截面由抛物线和矩形构成，矩形的长是，宽是，拱顶到地面的距离是，若以原点， 所在的直线为轴， 所在的直线为轴，建立平面直角坐标系．

    （）画出平面直角坐标系，并求出抛物线的函数表达式．

    （）在抛物线型拱壁， 处安装两盏灯，它们离地面的高度都是，则这两盏灯的水平距离是多少米？

    【答案】（）（）

    【解析】试题分析：（1）根据所建坐标系易求抛物线ADC的顶点坐标和A的坐标解答即可；
    （2）把y=8代入表达式中运用函数性质求解即可．

    试题解析：(1)画出直角坐标系xOy，如图：

    由题意可知,抛物线ADC的顶点坐标为(6,10)，

    A点坐标为(0,4)，

    可设抛物线ADC的函数表达式为

    将x=0,y=4代入得：

    ∴抛物线ADC的函数表达式为：

    (2)由y=8得：

    解得：

    则 即两盏灯的水平距离EF是米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

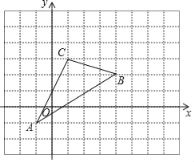
    【题目】如图，三角形ABC在直角坐标系中．

    （1）请直接写出点A、C两点的坐标：

    （2）三角形ABC的面积是　 　；

    （3）若把三角形ABC向上平移1个单位，再向右平移1个单位得三角形A′B′C′在图中画出三角形A′B′C’，这时点B′的坐标为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

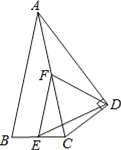
    【题目】如图，△ABC中，AB=AC，E、F分别是BC、AC的中点，以AC为斜边作Rt△ADC．

    （1）求证：FE=FD；

    （2）若∠CAD=∠CAB=24°，求∠EDF的度数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】受气候的影响，某超市蔬菜供应紧张，需每天从外地调运蔬菜1000斤．超市决定从甲、乙两大型蔬菜棚调运蔬菜，已知甲蔬菜棚每天最多可调出800斤，乙蔬菜棚每天最多可调运600斤，从两蔬菜棚调运蔬菜到超市的路程和运费如下表：

    到超市的路程（千米）

    运费（元/斤·千米）

    甲蔬菜棚

    120

    0.03

    乙蔬菜棚

    80

    0.05

    （1）若某天调运蔬菜的总运费为3840元，则从甲、乙两蔬菜棚各调运了多少斤蔬菜？

    （2）设从甲蔬菜棚调运蔬菜斤，总运费为元，试写出与的函数关系式，怎样安排调运方案才能使每天的总运费最省？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】快递配送员在一直在一条南北走向的街道上送快递，如果规定向北为正，向南为负，某天他从出发点开始所行走的路程记录为（单位：千米）：

    ＋10、－3、－5、＋4、＋6、＋5、－3、－6、－4、＋10

    (1) 在送快递过程中最远距出发点___________千米

    (2) 这天送完最后一个快递时，在出发点的什么方向，距离出发点是多少千米？

    (3) 如果送完快递后，需立即返回出发点，那么他这天送快递（含返回）共耗油多少升（已知每千米耗油0.2升）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，一次函数(为常数)的图象与反比例函数(为常数，且<0)的图象交于A，B两点．

    (1) 如图①，当，时，

    ① A ( ， )，B ( ， )；

    ②直接写出使成立的的取值范围；

    (2) 如图②，将(1)中直线AB向下平移，交反比例函数图像于点C，D，连接OC，AC，若△AOC的面积为8，求的值；

    (3) 若A，B两点的横坐标分别为，，且，满足，证明：2m-b=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并证明你的结论.

    ∠C与∠AED相等，理由如下：

    ∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)

    ∴∠2=___(___)，

    ∴AB∥EF(___)

    ∵∠3=___(___)

    又∠B=∠3(已知)

    ∴∠B=___(等量代换)

    ∴DE∥BC(___)

    ∴∠C=∠AED(___).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数的图象过点A（0，3）和点B（3，0），且与正比例函数的图象交于点P．

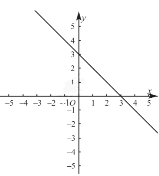
    （1）求函数的解析式和点P的坐标．

    （2）画出两个函数 的图象，并直接写出当时的取值范围．

    （3）若点Q是轴上一点，且△PQB的面积为8，求点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏，

    游戏规则：若一人出“剪刀”，另一人出“布”，则出“剪刀”者胜；若一人出“锤子”，另一人出“剪刀”，则出“锤子”者胜；若一人出“布”，另一人出“锤子”，则出“布”者胜，若两人出相同的手势，则两人平局.

    下列说法中错误的是

    A. 红红不是胜就是输，所以红红胜的概率为

    B. 红红胜或娜娜胜的概率相等

    C. 两人出相同手势的概率为

    D. 娜娜胜的概率和两人出相同手势的概率一样

    查看答案和解析>>

    同步练习册答案