
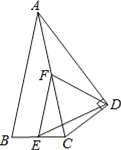
【题目】如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
(1)求证:FE=FD;
(2)若∠CAD=∠CAB=24°,求∠EDF的度数
【答案】(1)见解析;(2)54°.
【解析】试题分析:先根据题意判断出△DEF的形状,由平行线的性质得出∠EFC的度数,再由三角形外角的性质求出∠DFC的度数,再根据三角形内角和定理即可得出结论;
试题解析:
(1)证明:∵E、F分别是BC、AC的中点,
∴FE=![]() AB,
AB,
∵F是AC的中点,∠ADC=90°,
∴FD=![]() AC,
AC,
∵AB=AC,
∴FE=FD;
(2)解:∵E、F分别是BC、AC的中点,
∴FE∥AB,
∴∠EFC=∠BAC=24°,
∵F是AC的中点,∠ADC=90°,
∴FD=AF.
∴∠ADF=∠DAF=24°,
∴∠DFC=48°,
∴∠EFD=72°,
∵FE=FD,
∴∠FED=∠EDF=54°.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3)+7+(﹣6)+(﹣7)
(2)(-20)+(+3)-(-5)-(+7)
(3)(﹣3.5)×(﹣2)÷(- ![]() )÷(﹣5)
)÷(﹣5)
(4)﹣14+16÷(﹣2)3×|﹣3﹣1|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2![]() ,若∠EOF=45°,则F点的纵坐标是( )
,若∠EOF=45°,则F点的纵坐标是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣ ![]() ,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号).
,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
+1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,![]() ),(5,
),(5,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(﹣2,1),(3,![]() )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣ ![]() x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0). 
(1)求抛物线与直线AC的函数解析式;
(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;
(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B是反比例函数y= ![]() (k>0,x>0)图像上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图像大致为( )
(k>0,x>0)图像上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图像大致为( )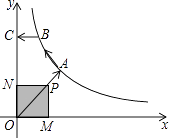
A.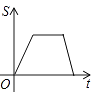
B.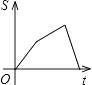
C.
D.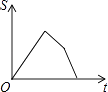
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com