
【题目】如图,二次函数y=ax2﹣ ![]() x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0). 
(1)求抛物线与直线AC的函数解析式;
(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;
(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标.
【答案】
(1)解:∵A(﹣4,0)在二次函数y=ax2﹣ ![]() x+2(a≠0)的图像上,
x+2(a≠0)的图像上,
∴0=16a+6+2,
解得a=﹣ ![]() ,
,
∴抛物线的函数解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+2;
x+2;
∴点C的坐标为(0,2),
设直线AC的解析式为y=kx+b,则
![]() ,
,
解得 ![]() ,
,
∴直线AC的函数解析式为: ![]()
(2)解:∵点D(m,n)是抛物线在第二象限的部分上的一动点,
∴D(m,﹣ ![]() m2﹣
m2﹣ ![]() m+2),
m+2),
过点D作DH⊥x轴于点H,
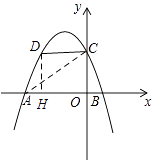
则DH=﹣ ![]() m2﹣
m2﹣ ![]() m+2,AH=m+4,HO=﹣m,
m+2,AH=m+4,HO=﹣m,
∵四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,
∴S= ![]() (m+4)×(﹣
(m+4)×(﹣ ![]() m2﹣
m2﹣ ![]() m+2)+
m+2)+ ![]() (﹣
(﹣ ![]() m2﹣
m2﹣ ![]() m+2+2)×(﹣m),
m+2+2)×(﹣m),
化简,得S=﹣m2﹣4m+4(﹣4<m<0)
(3)解:①若AC为平行四边形的一边,则C、E到AF的距离相等,
∴|yE|=|yC|=2,
∴yE=±2.
当yE=2时,解方程﹣ ![]() x2﹣
x2﹣ ![]() x+2=2得,
x+2=2得,
x1=0,x2=﹣3,
∴点E的坐标为(﹣3,2);
当yE=﹣2时,解方程﹣ ![]() x2﹣
x2﹣ ![]() x+2=﹣2得,
x+2=﹣2得,
x1= ![]() ,x2=
,x2= ![]() ,
,
∴点E的坐标为( ![]() ,﹣2)或(
,﹣2)或( ![]() ,﹣2);
,﹣2);
②若AC为平行四边形的一条对角线,则CE∥AF,
∴yE=yC=2,
∴点E的坐标为(﹣3,2).
综上所述,满足条件的点E的坐标为(﹣3,2)、( ![]() ,﹣2)、(
,﹣2)、( ![]() ,﹣2).
,﹣2).
【解析】(1)把点A的坐标代入抛物线的解析式,就可求得抛物线的解析式,根据A,C两点的坐标,可求得直线AC的函数解析式;(2)先过点D作DH⊥x轴于点H,运用割补法即可得到:四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,据此列式计算化简就可求得S关于m的函数关系;(3)由于AC确定,可分AC是平行四边形的边和对角线两种情况讨论,得到点E与点C的纵坐标之间的关系,然后代入抛物线的解析式,就可得到满足条件的所有点E的坐标.
【考点精析】本题主要考查了公式法和平行四边形的性质的相关知识点,需要掌握要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,△AOB中,A(-8,0),B(0, ![]() ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F,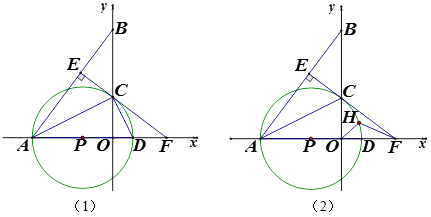
(1)求⊙P的半径;
(2)求证:EF为⊙P的切线;
(3)若点H是 ![]() 上一动点,连接OH、FH,当点P在
上一动点,连接OH、FH,当点P在 ![]() 上运动时,试探究
上运动时,试探究 ![]() 是否为定值?若为定值,求其值;若不是定值,请说明理由.
是否为定值?若为定值,求其值;若不是定值,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
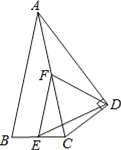
【题目】如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
(1)求证:FE=FD;
(2)若∠CAD=∠CAB=24°,求∠EDF的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx﹣4与x轴交于A,B两点,(点B在点A的右侧)且A,B两点的坐标分别为(﹣2,0)、(8,0),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)在(2)的结论下,试问抛物线上是否存在点N(不同于点Q),使三角形BCN的面积等于三角形BCQ的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD分别表示两幢相距36米的大楼,高兴同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°,求大楼AB的高. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车厂计划半年内每月生产汽车20辆,由于另有任务,每月上班人数不一定相等,实每月生产量与计划量相比情况如下表(增加为正,减少为负)

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)半年内总生产量是多少?比计划多了还是少了,增加或减少多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一张纸片ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿BG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( ) 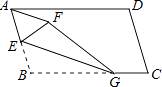
A.∠FEG
B.∠EAF
C.∠AEF
D.∠EFA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a=2016×2018-2016×2017, b=2015×2016-2013×2017,![]() ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
A. a<b<c B. a<c<b C. b<a<c D. b<c<a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com