[题目]某汽车厂计划半年内每月生产汽车20辆.由于另有任务.每月上班人数不一定相等.实每月生产量与计划量相比情况如下表(1)生产量最多的一天比生产量最少的一天多生产多少辆?(2)半年内总生产量是多少?比计划多了还是少了.增加或减少多少? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月上班人数不一定相等，实每月生产量与计划量相比情况如下表（增加为正，减少为负）

(1)生产量最多的一天比生产量最少的一天多生产多少辆？

(2)半年内总生产量是多少？比计划多了还是少了，增加或减少多少？

【答案】（1）生产量最多的一天比生产量最少的一天多生产9辆；（2）半年内总生产量是121辆。比计划多了1辆.

【解析】

（1）由表格可知，四月生产最多为：20+4=24；六月最少为：20-5=15，两者相减即可求解；
（2）把每月的生产量加起来即可，然后与计划相比较.

（1）+4－（－5）=9（辆）

答：生产量最多的一天比生产量最少的一天多生产9辆.

（2）20×6+［+3+(－2)+(－1)+(+4)+(+2)+(－5)］=120+(+1)=121（辆），

因为121＞120 121-120=1（辆）

答：半年内总生产量是121辆。比计划多了1辆.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，平行四边形ABCD中，AB=8cm，AD=12cm，点P在AD边上以每秒1cm 的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动以后，以P、D、Q、B四点组成平行四边形的次数有__次．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】观察下列两个等式：2﹣＝2×+1，5﹣＝5×+1，给出定义如下：我们称使等式a﹣b＝ab+1的成立的一对有理数a，b为“共生有理数对”，记为（a，b），如：数对（2，），（5，），都是“共生有理数对”．

（1）数对（﹣2，1），（3，）中是“共生有理数对”的是　　；

（2）若（m，n）是“共生有理数对”，则（﹣n，﹣m）　　“共生有理数对”（填“是”或“不是”）；

（3）请再写出一对符合条件的“共生有理数对”为　　；（注意：不能与题目中已有的“共生有理数对”重复）

（4）若（a，3）是“共生有理数对”，求a的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

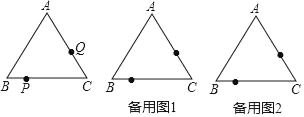
【题目】如图，△ABC是边长为6cm的等边三角形．若点P以1cm/s的速度从点B出发，同时点Q以1.5cm/s的速度从点C出发，都按逆时针方向沿△ABC的边运动，运动时间为6秒．

（1）试求出运动到多少秒时，直线PQ与△ABC的某边平行；

（2）当运动到t1秒时，P、Q对应的点为P1、Q1，当运动到t2秒时（t1≠t2），P、Q对应的点为P2、Q2，试问：△P1CQ1与△P2CQ2能否全等？若能，求出t1、t2的值；若不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，二次函数y=ax2﹣ x+2（a≠0）的图像与x轴交于A、B两点，与y轴交于点C，已知点A（﹣4，0）．
（1）求抛物线与直线AC的函数解析式；
（2）若点D（m，n）是抛物线在第二象限的部分上的一动点，四边形OCDA的面积为S，求S关于m的函数关系；
（3）若点E为抛物线上任意一点，点F为x轴上任意一点，当以A、C、E、F为顶点的四边形是平行四边形时，请直接写出满足条件的所有点E的坐标．