【题目】如图，在□ABCD中，点E，F分别是边AB，CD的中点，(1)求证：△CFB≌△AED；
（2）若∠ADB＝90°，判断四边形BFDE的形状，并说明理由；
【答案】(1)见解析;(2) 四边形BFDE是菱形.
【解析】分析：（1）首先根据平行四边形的性质，得到相等的边角和平行线，然后根据中点的性质和全等三角形的判定SAS证明即可；
（2）连接EF，根据一组对边平行且相等的四边形是平行四边形证得：四边形四边形
是平行四边形，四边形
是平行四边形，然后根据平行线的性质证明，最后得到对角线互相垂直的平行四边形是菱形.
详解：(1)证明：
四边形
是平行四边形
∴
，
，
又∵点E,F分别是AB，CD的中点
∴
∴
（2）解法一：四边形
是菱形。证明如下：
连接EF
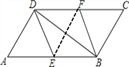
∵四边形是平行四边形
∴
又∵点E,F分别是AB，CD的中点
∴
∴四边形是平行四边形
同理，四边形是平行四边形
∴
∴
∴
∴四边形是菱形。
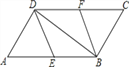
（2）解法二：四边形是菱形。证明如下：
∵四边形是平行四边形
∴
又∵点E,F分别是AB，CD的中点
∴
,
∴四边形是平行四边形
又∵
∴在
中，
∴四边形是菱形。
寒假创新型自主学习第三学期寒假衔接系列答案科目：初中数学 来源： 题型：
【题目】某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月上班人数不一定相等，实每月生产量与计划量相比情况如下表（增加为正，减少为负）
(1)生产量最多的一天比生产量最少的一天多生产多少辆？
(2)半年内总生产量是多少？比计划多了还是少了，增加或减少多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
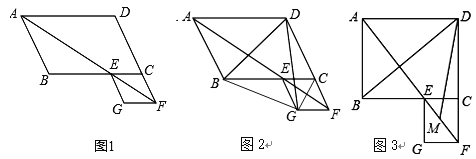
【题目】在□ABCD中，∠BAD的平分线交直线BC于点E，交直线DC的延长线于点F，以EC、CF为邻边作□ECFG．
（1）如图1，证明□ECFG为菱形；
（2）如图2，若∠ABC=120°，连接BG、CG，求证△DGC≌△BGE，并求出∠BDG的度数；
（3）如图3，若∠ABC=90°，M是EF的中点，请直接写出∠BDM的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
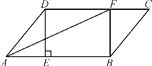
【题目】如图，在□ABCD中，过点D作DE⊥AB于点E，点F在边CD上，CF＝AE，连接AF，BF.
（1）求证：四边形BFDE是矩形
（2）若CF＝6，BF＝8，DF＝10，求证：AF是∠DAB的平分线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若a＝2016×2018－2016×2017， b＝2015×2016－2013×2017，
，则a，b，c的大小关系是( )
A. a＜b＜c B. a＜c＜b C. b＜a＜c D. b＜c＜a
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请观察下列算式，找出规律并填空。
，
，
，
···
根据以上规律解答以下三题：
(1) 第10个等式是:__________=_____________
第n个等式是:__________=_____________
(2)计算：
的值。
(3)若有理数
满足
,试求：
的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
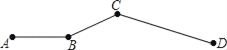
【题目】如图，老王开车从A到D，全程共72千米．其中AB段为平地，车速是30千米/小时，BC段为上山路，车速是22.5千米/小时，CD段为下山路，车速是36千米/小时，已知下山路是上山路的2倍．
（1）若AB=6千米，老王开车从A到D共需多少时间？
（2）当BC的长度在一定范围内变化时，老王开车从A到D所需时间是否会改变？为什么？（给出计算过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD．
(1)、求证：四边形AODE是矩形；(2)、若AB＝6，∠BCD＝120°，求四边形AODE的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
