
【题目】在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作□ECFG.
(1)如图1,证明□ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,求证△DGC≌△BGE,并求出∠BDG的度数;
(3)如图3,若∠ABC=90°,M是EF的中点,请直接写出∠BDM的度数.
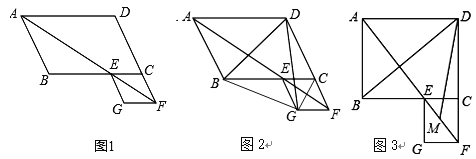
【答案】(1)证明见解析;(2)∠BDG=60°;(3)∠BDM=45°
【解析】分析:(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形;
(2)延长AB、FG交于H,连接HD,求证平行四边形AHFD为菱形,得出△ADH,△DHF为全等的等边三角形,证明△BHD≌△GFD,即可得出答案;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到∠BDM的度数.
解:(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴□ECFG为菱形.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD

∴∠BAD+∠ABC=180°,∠BCF=∠ABC,∠DAF=∠AEB,
∵∠ABC=120°,
∴∠BAD=60°,∠BCF=120°,
∵AF平分∠BAD,
∴∠BAF=∠DAE=30°,
∴∠BAF=∠BEA=30°,
∴AB=BE,
∴BE=CD,
∵四边形ECFG为菱形,且∠BCF=120°
∴△ECG,△GCF为全等的等边三角形,
∴GE=GC,∠GEC=∠GCE=60°,
∴∠BEG=∠DCG=120°,
∴△DGC≌△BGE(SAS),
∴∠BGE=∠DGC,BG=DG
∴∠BGD=∠BGE+∠EGD=∠DGC+∠EGD=60°,
∴△BGD是等边三角形,
∴∠BDG=60°;
(3)如图2,∠BDM=45°;

如图,连接BM,MC,
∵∠ABC=90,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵ ,
,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形,
∴∠BDM=45°.


科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
+1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,![]() ),(5,
),(5,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(﹣2,1),(3,![]() )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦用8万元购进纪念运动休闲衫,面市后供不应求,商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元,商厦销售这种运动休闲衫时每件定价都是58元,最后剩下的150件按八折销售,很快售完.
(1)商厦第一批和第二批各购进休闲衫多少件?
(2)请问在这两笔生意中,商厦共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七![]() 班派出
班派出![]() 名同学参加数学竞赛,老师以
名同学参加数学竞赛,老师以![]() 分为基准,把分数超过
分为基准,把分数超过![]() 分的部分记为正数,不足部分记为负数.评分记录如下:
分的部分记为正数,不足部分记为负数.评分记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 这
这![]() 名同学中最高分和最低分各是多少?
名同学中最高分和最低分各是多少?
![]() 超过基准分的和低于基准分的各有多少人?
超过基准分的和低于基准分的各有多少人?
![]() 这十二名同学的平均成绩是多少?
这十二名同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B是反比例函数y= ![]() (k>0,x>0)图像上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图像大致为( )
(k>0,x>0)图像上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图像大致为( )
A.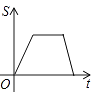
B.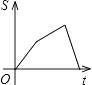
C.
D.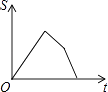
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)若-1表示的点与5表示的点重合,回答以下问题:
① 7表示的点与数 表示的点重合;
② 若数轴上A、B两点之间的距离为11(A在B的左侧),且A、B两点经折叠后
重合, 求A、B两点表示的数各是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E,F分别是边AB,CD的中点,(1)求证:△CFB≌△AED;
(2)若∠ADB=90°,判断四边形BFDE的形状,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=5,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

请回答:BC+DE的值为________
参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠AGF的度数________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com