
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
+1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,![]() ),(5,
),(5,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(﹣2,1),(3,![]() )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
【答案】(1)(3,![]() )是“共生有理数对”;(2)是(3)(4,
)是“共生有理数对”;(2)是(3)(4,![]() )或(6,
)或(6,![]() )等;(4)a=﹣2
)等;(4)a=﹣2
【解析】
(1)计算后,根据“共生有理数对”的定义判定即可;(2)根据(m,n)是“共生有理数对”可得m-n=mn+1,根据根据“共生有理数对”的定义即可证明;(3)根据“共生有理数对”的定义写出符合条件的数对即可(注意:不能与题目中已有的“共生有理数对”重复);(4)根据“共生有理数对”的定义可得a-(-3)=-3a+1,由此即可求得a值.
(1)-2-1=-3,(-2) ×1+1=-1,-3≠-1,故(-2,1)不是共生有理数对;3-![]() =
=![]() ,3×
,3×![]() +1=
+1=![]() ,故(3,
,故(3,![]() )是共生有理数对;
)是共生有理数对;
故答案为:(3,![]() );
);
(2)是.
理由: -n-(-m)=-n+m,-n×(-m)+1=mn+1 ,
∵(m,n)是“共生有理数对”
∴m-n=mn+1,
∴-n+m=mn+1,
∴(-n,-m)是“共生有理数对”;
(3)(4,![]() )或6,
)或6,![]() )等(答案不唯一,只要不和题中重复即可);
)等(答案不唯一,只要不和题中重复即可);
(4)由题意可知,a-(-3)=-3a+1,
解得a=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知图所示的计算程序.
![]()
根据计算程序回答下列问题:
(1)填写表内空格:
输入x | 3 | 2 | -2 |
| … |
输出答案 | 0 | … |
(2)你发现的规律是 .
(3)用简要过程说明你发现的规律的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为 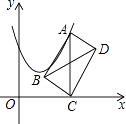
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为 ;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
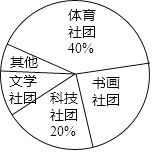
查看答案和解析>>
科目:初中数学 来源: 题型:
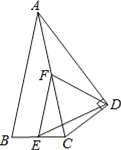
【题目】如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
(1)求证:FE=FD;
(2)若∠CAD=∠CAB=24°,求∠EDF的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
(1)求证:四边形PMEN是平行四边形;
(2) 当AP为何值时,四边形PMEN是菱形?并给出证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx﹣4与x轴交于A,B两点,(点B在点A的右侧)且A,B两点的坐标分别为(﹣2,0)、(8,0),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交BD于点M.
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)在(2)的结论下,试问抛物线上是否存在点N(不同于点Q),使三角形BCN的面积等于三角形BCQ的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车厂计划半年内每月生产汽车20辆,由于另有任务,每月上班人数不一定相等,实每月生产量与计划量相比情况如下表(增加为正,减少为负)

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)半年内总生产量是多少?比计划多了还是少了,增加或减少多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
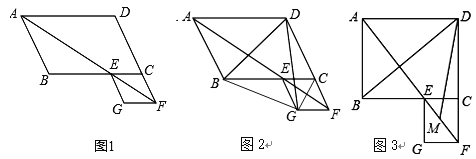
【题目】在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作□ECFG.
(1)如图1,证明□ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,求证△DGC≌△BGE,并求出∠BDG的度数;
(3)如图3,若∠ABC=90°,M是EF的中点,请直接写出∠BDM的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com