
【题目】如图,已知一张纸片ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿BG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( ) 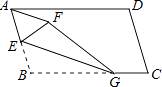
A.∠FEG
B.∠EAF
C.∠AEF
D.∠EFA
科目:初中数学 来源: 题型:
【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2![]() ,若∠EOF=45°,则F点的纵坐标是( )
,若∠EOF=45°,则F点的纵坐标是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣ ![]() x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
x+2(a≠0)的图像与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0). 
(1)求抛物线与直线AC的函数解析式;
(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;
(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦用8万元购进纪念运动休闲衫,面市后供不应求,商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元,商厦销售这种运动休闲衫时每件定价都是58元,最后剩下的150件按八折销售,很快售完.
(1)商厦第一批和第二批各购进休闲衫多少件?
(2)请问在这两笔生意中,商厦共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题: 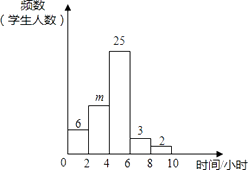
(1)求m的值;
(2)计算50名学生的课外活动时间的平均数(每组时间用其组中值表示),对初三年级全体学生平均每周的课外活动吋问做个推断;
(3)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表法,求其中至少有1人课外活动时间在8~10小时的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七![]() 班派出
班派出![]() 名同学参加数学竞赛,老师以
名同学参加数学竞赛,老师以![]() 分为基准,把分数超过
分为基准,把分数超过![]() 分的部分记为正数,不足部分记为负数.评分记录如下:
分的部分记为正数,不足部分记为负数.评分记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 这
这![]() 名同学中最高分和最低分各是多少?
名同学中最高分和最低分各是多少?
![]() 超过基准分的和低于基准分的各有多少人?
超过基准分的和低于基准分的各有多少人?
![]() 这十二名同学的平均成绩是多少?
这十二名同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B是反比例函数y= ![]() (k>0,x>0)图像上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图像大致为( )
(k>0,x>0)图像上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图像大致为( )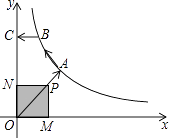
A.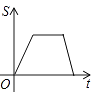
B.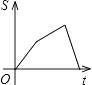
C.
D.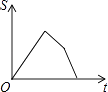
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22016的值,可设S=1+2+22+23+…+22016 , 于是2S=2+22+23+…+22017 , 因此2S﹣S=22017﹣1,所以S=22017﹣1.我们把这种求和方法叫错位相减法.仿照上述的思路方法,计算出1+5+52+53+…+52016的值为( )
A.52017﹣1
B.52016﹣1
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com