
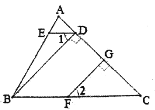
【题目】如图所示,BD⊥AC于点D,FG⊥AC于点G,∠1=∠2,试证明:∠ADE=∠C
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
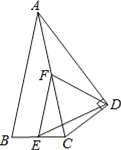
【题目】如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
(1)求证:FE=FD;
(2)若∠CAD=∠CAB=24°,求∠EDF的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.

∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=___(___),
∴AB∥EF(___)
∵∠3=___(___)
又∠B=∠3(已知)
∴∠B=___(等量代换)
∴DE∥BC(___)
∴∠C=∠AED(___).
查看答案和解析>>
科目:初中数学 来源: 题型:
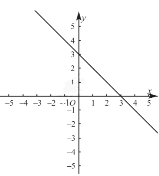
【题目】已知一次函数![]() 的图象过点A(0,3)和点B(3,0),且与正比例函数
的图象过点A(0,3)和点B(3,0),且与正比例函数![]() 的图象交于点P.
的图象交于点P.
(1)求函数![]() 的解析式和点P的坐标.
的解析式和点P的坐标.
(2)画出两个函数 的图象,并直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
(3)若点Q是![]() 轴上一点,且△PQB的面积为8,求点Q的坐标.
轴上一点,且△PQB的面积为8,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
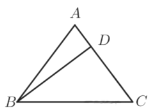
(1)判断△BCD的形状并证明你的结论.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠A=∠C,AD平分∠BDF.
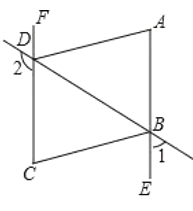
(1)AE与FC的位置关系如何?为什么?
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.
下列说法中错误的是
A. 红红不是胜就是输,所以红红胜的概率为![]()
B. 红红胜或娜娜胜的概率相等
C. 两人出相同手势的概率为![]()
D. 娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.

(1)当∠AOB=30°时,求弧AB的长;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com