
【题目】如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.

(1)当∠AOB=30°时,求弧AB的长;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.
【答案】![]() ;3;存在
;3;存在
【解析】
试题分析:(1)连结BC,
∵A(10,0),∴OA=10,CA=5,
∵∠AOB=30°,
∴∠ACB=2∠AOB=60°,
∴弧AB的长=![]() ;……4分
;……4分
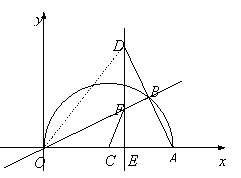

(2)连结OD,
∵OA是⊙C直径,∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=10,
在Rt△ODE中,
OE=![]()
![]() ,
,
∴AE=AO-OE=10-6=4,
由∠AOB=∠ADE=90°-∠OAB,∠OEF=∠DEA,
得△OEF∽△DEA,
∴![]() ,即
,即![]() ,∴EF=3;……8分
,∴EF=3;……8分
(3)设OE=x,
①当交点E在O,C之间时,由以点E、C、F为顶点的三角形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,当∠ECF=∠BOA时,此时△OCF为等腰三角形,点E为OC中点,即OE=![]() ,
,
∴E1(![]() ,0);
,0);
当∠ECF=∠OAB时,有CE=5-x,AE=10-x,
∴CF∥AB,有CF=![]() ,
,
∵△ECF∽△EAD,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
∴E2(![]() ,0);
,0);
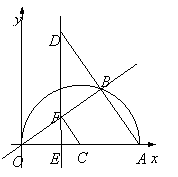
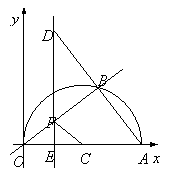
②当交点E在点C的右侧时,
∵∠ECF>∠BOA,
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO,
连结BE,
∵BE为Rt△ADE斜边上的中线,
∴BE=AB=BD,
∴∠BEA=∠BAO,
∴∠BEA=∠ECF,
∴CF∥BE,∴![]() ,
,
∵∠ECF=∠BAO,∠FEC=∠DEA=Rt∠,
∴△CEF∽△AED,∴![]() ,
,
而AD=2BE,∴![]() ,
,
即![]() ,解得
,解得![]() ,
,![]() <0(舍去),
<0(舍去),
∴E3(![]() ,0);
,0);
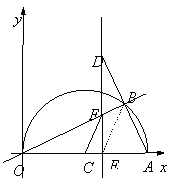

③当交点E在点O的左侧时,
∵∠BOA=∠EOF>∠ECF.
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO
连结BE,得BE=![]() =AB,∠BEA=∠BAO
=AB,∠BEA=∠BAO
∴∠ECF=∠BEA,
∴CF∥BE,
∴![]() ,
,
又∵∠ECF=∠BAO,∠FEC=∠DEA=Rt∠,
∴△CEF∽△AED,∴![]() ,
,
而AD=2BE,∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() <0(舍去),
<0(舍去),
∵点E在x轴负半轴上,∴E4(![]() ,0),
,0),
综上所述:存在以点E、C、F为顶点的三角形与△AOB相似,此时点E坐标为:
![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0)、
,0)、![]() (
(![]() ,0).(12分)
,0).(12分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
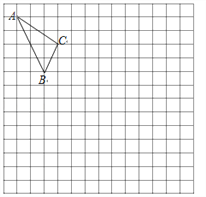
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形![]() (顶点是网格线交点的三角形)的顶点
(顶点是网格线交点的三角形)的顶点![]() 的坐标分别是
的坐标分别是![]() .
.
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的周长最小,并写出点
的周长最小,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(-1,y1),(2,y2),(3,y3)在反比例函数![]() 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y1>y2 D. y2>y3>y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]()
(1)请直接写出方程![]() 的所有正整数解
的所有正整数解
(2)若方程组的解满足x+y=0,求m的值
(3)无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,请直接写出这个解?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:
①![]()
② -10 - (-31)
③1÷(﹣![]() )×
)×![]() ;
;
④(-2)2×5+(-2)3÷4
⑤![]()
(2)比较大小
①1.5与4 ②2与-7
③![]() 与
与![]() ④
④ ![]() 与
与![]()
(3)用简便方法计算:
①![]()
②![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com