
【题目】如图,已知A,O,E三点在一条直线上,OB平分∠AOC,∠AOB+∠DOE=90°,试问:∠COD与∠DOE之间有怎样的关系?说明理由.-com 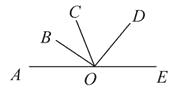
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】下列式子正确的是( )
A.x﹣(y﹣z)=x﹣y﹣z
B.﹣(x﹣y+z)=﹣x﹣y﹣z
C.x+2y﹣2z=x﹣2(z+y)
D.﹣a+c+d+b=﹣(a﹣b)﹣(﹣c﹣d)
查看答案和解析>>
科目:初中数学 来源: 题型:
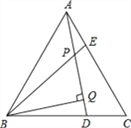
【题目】如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.PQ=4,PE=1
(1)求证:△ABE≌△CAD;
(2)求∠BPQ的度数.
(3)求AD的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com