
【题目】如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于P.PQ=4,PE=1
(1)求证:△ABE≌△CAD;
(2)求∠BPQ的度数.
(3)求AD的长。
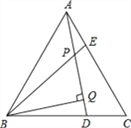
【答案】(1)见解析(2)60°;(3)9
【解析】【试题分析】
(1)根据等边三角形的性质,易得AB=AC,∠BAC=∠C=60°,因为AE=CD,根据SAS判定,易得△ABE≌△CAD;
(2)根据全等三角形的性质得,∠ABE=∠CAD,利用等量代换得:∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°;
(3) 在![]() 中,
中, ![]() 因为 PQ=4,所以BP=8,由于PE=1,所以BE=BP+PE=8+1=9,因为AD=BE,所以 AD=9.
因为 PQ=4,所以BP=8,由于PE=1,所以BE=BP+PE=8+1=9,因为AD=BE,所以 AD=9.
【试题解析】
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE与△CAD中,
AB=AC,∠BAC=∠C=60°,AE=CD,
∴△ABE≌△CAD(SAS);
(2)由(1)知△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°.
(3)在![]() 中,
中, ![]()
![]() PQ=4,
PQ=4, ![]() ,
,
![]() BP=8,由于PE=1,
BP=8,由于PE=1,
![]() BE=BP+PE=8+1=9,
BE=BP+PE=8+1=9, ![]() AD=BE,
AD=BE, ![]() AD=9.
AD=9.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】如图,下列各语句中,错误的语句是( ) 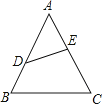
A.∠ADE与∠B是同位角
B.∠BDE与∠C是同旁内角
C.∠BDE与∠AED是内错角
D.∠BDE与∠DEC是同旁内角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,O,E三点在一条直线上,OB平分∠AOC,∠AOB+∠DOE=90°,试问:∠COD与∠DOE之间有怎样的关系?说明理由.-com 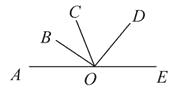
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则该正方形内,这张圆形纸片“不能接触到的部分”的面积是( ) 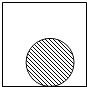
A.a2﹣π
B.(4﹣π)a2
C.π
D.4﹣π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com