
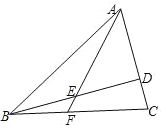
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.
【答案】(1)∠EAD的余切值为![]() ;(2)
;(2)![]() =
=![]() .
.
【解析】
(1)在Rt△ADB中,根据AB=13,cos∠BAC=![]() ,求出AD的长,由勾股定理求出BD的长,进而可求出DE的长,然后根据余切的定义求∠EAD的余切即可;
,求出AD的长,由勾股定理求出BD的长,进而可求出DE的长,然后根据余切的定义求∠EAD的余切即可;
(2)过D作DG∥AF交BC于G,由平行线分线段成比例定理可得CD:AD=CG:FG=3:5,从而可设CD=3x,AD=5x,再由EF∥DG,BE=ED, 可知BF=FG=5x,然后可求BF:CF的值.
(1)∵BD⊥AC,
∴∠ADE=90°,
Rt△ADB中,AB=13,cos∠BAC=![]() ,
,
∴AD=5, 由勾股定理得:BD=12,
∵E是BD的中点,
∴ED=6,
∴∠EAD的余切=![]() =
=![]() ;
;
(2)过D作DG∥AF交BC于G,
∵AC=8,AD=5, ∴CD=3,
∵DG∥AF,
∴![]() =
=![]() ,
,
设CD=3x,AD=5x,
∵EF∥DG,BE=ED,
∴BF=FG=5x,
∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校选拔射击运动员参加比赛,甲、乙两人在相同的条件下连续射靶各![]() 次,命中的环数(均为不大于10的正整数)如表:
次,命中的环数(均为不大于10的正整数)如表:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
(1)当![]() 为何值时,选派乙去参加比赛更合适,请说明理由;
为何值时,选派乙去参加比赛更合适,请说明理由;
(2)若乙最后两次射靶均命中![]() 环,则选派谁去参加比赛更合适?请说明理由.
环,则选派谁去参加比赛更合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店有![]() 两种商品,已知在打折前,买
两种商品,已知在打折前,买![]() 件
件![]() 商品和
商品和![]() 件
件![]() 商品用了
商品用了![]() 元,买
元,买![]() 件
件![]() 商品和
商品和![]() 件
件![]() 商品用了
商品用了![]() 元.
元.![]() 两种商品打相同折以后,某人买
两种商品打相同折以后,某人买![]() 件
件![]() 商品和
商品和![]() 件
件![]() 商品一共比不打折少花
商品一共比不打折少花![]() 元,请问
元,请问![]() 两种商品打折前各多少钱?打了多少折?
两种商品打折前各多少钱?打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
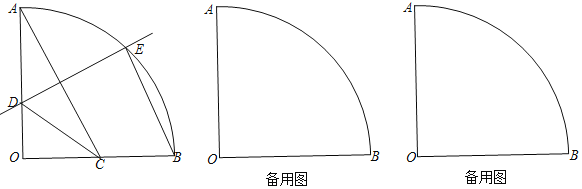
【题目】已知:如图,在半径为2的扇形![]() 中,
中,![]() °,点C在半径OB上,AC的垂直平分线交OA于点D,交弧AB于点E,联结
°,点C在半径OB上,AC的垂直平分线交OA于点D,交弧AB于点E,联结![]() .
.
(1)若C是半径OB中点,求![]() 的正弦值;
的正弦值;
(2)若E是弧AB的中点,求证:![]() ;
;
(3)联结CE,当△DCE是以CD为腰的等腰三角形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知![]() ,AC=5,那么△DBF的面积等于_____.
,AC=5,那么△DBF的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.

(1)当x的取值为 时,在甲乙两家店所花钱一样多?
(2)当x的取值为 时,在乙店批发比较便宜?
(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com