
【题目】某校选拔射击运动员参加比赛,甲、乙两人在相同的条件下连续射靶各![]() 次,命中的环数(均为不大于10的正整数)如表:
次,命中的环数(均为不大于10的正整数)如表:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
(1)当![]() 为何值时,选派乙去参加比赛更合适,请说明理由;
为何值时,选派乙去参加比赛更合适,请说明理由;
(2)若乙最后两次射靶均命中![]() 环,则选派谁去参加比赛更合适?请说明理由.
环,则选派谁去参加比赛更合适?请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ,理由见解析;(2)甲同学的成绩较稳定,应选甲参加比赛,理由见解析
,理由见解析;(2)甲同学的成绩较稳定,应选甲参加比赛,理由见解析
【解析】
(1)利用平均数的计算公式,分别计算甲、乙两名同学射击环数的平均数,根据乙的平均数大于甲的平均数时派乙比赛合适,列出不等式,解不等式并且取正整数解即可;
(2)当m=0时,甲、乙两名同学射击环数的平均数相同,所以利用方差的计算公式计算方差,因为方差小的成绩稳定,故选方差小的运动员比赛.
(1)![]() ,
,
![]() ,
,
若选派乙去参加比赛更合适,则![]() ,
,
解得:![]() ,
,
因为![]() 为正整数,
为正整数,
所以![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)当![]() 时,
时,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
∴因为甲、乙两名同学射击环数的平均数相同,乙同学射击的方差大于甲同学的方差,
∴甲同学的成绩较稳定,应选甲参加比赛.


科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(
的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(![]() ,y1),(
,y1),(![]() ,y2)是抛物线上两点,则y1<y2,其中正确的结论有( )个
,y2)是抛物线上两点,则y1<y2,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,以点
边上,以点![]() 为圆心
为圆心![]() 为半径作弧交边
为半径作弧交边![]() 于点
于点![]() ,射线
,射线![]() 与射线
与射线![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的长;
的长;
(2)联结![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得△
,使得△![]() 与△
与△![]() 相似,若相似,求
相似,若相似,求![]() 的值,若不相似,请说明理由
的值,若不相似,请说明理由
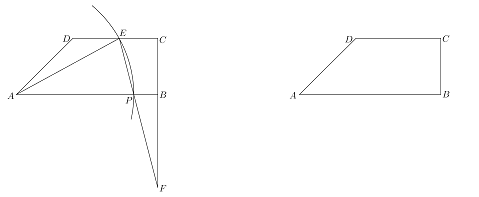
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 边上的两动点,且在运动过程中保持
边上的两动点,且在运动过程中保持![]() ,
,![]() 为
为![]() 的对角线.
的对角线.
(1)如图①,若![]() ,
,

图①
①当点![]() 与点
与点![]() 重合时,探索
重合时,探索![]() 的值;
的值;
②当点![]() 与点
与点![]() 不重合时,探索
不重合时,探索![]() 的值;
的值;
(2)如图②,参考(1)研究方法,若![]() ,
,

图②
①当点![]() 与点
与点![]() 重合时,探索
重合时,探索![]() 的值;
的值;
②当点![]() 与点
与点![]() 不重合时,探索
不重合时,探索![]() 的值;
的值;
(3)如图③,参考(1)(2)研究方法,若![]() 时,试探索是否存在常数
时,试探索是否存在常数![]() ,使得
,使得![]() ,若存在,请直接写出
,若存在,请直接写出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
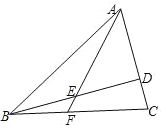
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=5,BC=6,点O是边BC上的动点,以点O为圆心,OB为半径作圆O,交AB边于点D,过点D作∠ODP=∠B,交边AC于点P,交圆O与点E.设OB=x.
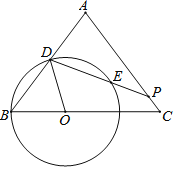
(1)当点P与点C重合时,求PD的长;
(2)设AP﹣EP=y,求y关于x的解析式及定义域;
(3)联结OP,当OP⊥OD时,试判断以点P为圆心,PC为半径的圆P与圆O的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com