
【题目】已知在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 边上的两动点,且在运动过程中保持
边上的两动点,且在运动过程中保持![]() ,
,![]() 为
为![]() 的对角线.
的对角线.
(1)如图①,若![]() ,
,

图①
①当点![]() 与点
与点![]() 重合时,探索
重合时,探索![]() 的值;
的值;
②当点![]() 与点
与点![]() 不重合时,探索
不重合时,探索![]() 的值;
的值;
(2)如图②,参考(1)研究方法,若![]() ,
,

图②
①当点![]() 与点
与点![]() 重合时,探索
重合时,探索![]() 的值;
的值;
②当点![]() 与点
与点![]() 不重合时,探索
不重合时,探索![]() 的值;
的值;
(3)如图③,参考(1)(2)研究方法,若![]() 时,试探索是否存在常数
时,试探索是否存在常数![]() ,使得
,使得![]() ,若存在,请直接写出
,若存在,请直接写出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

【答案】(1)①![]() ;②
;②![]() ;
;
(2)①![]() ;②
;②![]() ;
;
(3)![]() .
.
【解析】
(1)①利用等边三角形的性质即可解决问题;
②如图①中,只要证明![]() 即可解决问题;
即可解决问题;
(2)①解直角三角形求出有关线段即可解决问题;②若点![]() 与点
与点![]() 不重合,如图②中,过点
不重合,如图②中,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,只要证明
,只要证明![]() ,可得
,可得![]() ,在
,在![]() 中,
中,![]() ,可得
,可得![]() ,
,![]() ,推出
,推出![]() ,在
,在![]() 中,由
中,由![]() ,可得
,可得![]() ,由此即可解决问题;
,由此即可解决问题;
(3)模仿(1)(2)的解法即可解决问题;
解;(1)①如图①﹣1中,

图①-1
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]()
![]()
![]()
![]() ,
,![]() 都是等边三角形
都是等边三角形
![]()
![]()
![]() 点
点![]() 与点
与点![]() 重合
重合
![]() 点
点![]() 与点
与点![]() 重合
重合
![]() ,
,![]()
![]()
![]() .
.
②若点![]() 与点
与点![]() 不重合.如图①中,
不重合.如图①中,

图①
由①得![]() ,
,![]() 都是等边三角形
都是等边三角形
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)①若点![]() 与点
与点![]() 重合,如图②﹣1中,
重合,如图②﹣1中,

图②-1
![]() ,
,![]()
易知![]() ,又
,又![]() ,
,![]()
![]() 又
又![]()
![]()
容易证得![]()
设![]() ,则
,则![]() ,
,![]() ,
,
又![]() ,
,
![]() .
.
若点![]() 与点
与点![]() 不重合,如图②中,过点
不重合,如图②中,过点![]() 作
作![]() 于点
于点![]() ,
,
设![]() ,
,

图②
由上可知![]() ,
,
![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
(3)如图③当点![]() 与
与![]() 重合时,作
重合时,作![]() 于
于![]() ,
,![]() 于
于![]() .
.
设![]() ,
,![]() .
.

图③
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
由(1)(2)可知:当点![]() 与点
与点![]() 不重合时,
不重合时,![]() ,
,
综上所述,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
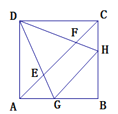
【题目】在正方形ABCD中,点G在AB上,点H在BC上,且∠GDH=45°,DG、DH分别与对角线AC交于点E、F,则线段AE、EF、FC之间的数量关系为_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 与一次函数
与一次函数![]() (k≠0),一次函数的图象与y轴交于点C,与x轴交于点D.
(k≠0),一次函数的图象与y轴交于点C,与x轴交于点D.
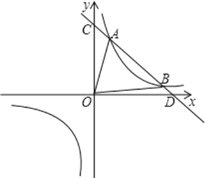
(1)当k=-1时,如图,设直线![]() 与双曲线
与双曲线![]() 的两个交点为A、B(B在A的右边),求△OAB的面积;
的两个交点为A、B(B在A的右边),求△OAB的面积;
(2)若直线![]() 与双曲线
与双曲线![]() 总有两个不同的交点,求k的取值范围;
总有两个不同的交点,求k的取值范围;
(3)若直线![]() 与双曲线
与双曲线![]() 交于不同的两点M(
交于不同的两点M(![]() )、N(
)、N(![]() ),且满足
),且满足![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校选拔射击运动员参加比赛,甲、乙两人在相同的条件下连续射靶各![]() 次,命中的环数(均为不大于10的正整数)如表:
次,命中的环数(均为不大于10的正整数)如表:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
(1)当![]() 为何值时,选派乙去参加比赛更合适,请说明理由;
为何值时,选派乙去参加比赛更合适,请说明理由;
(2)若乙最后两次射靶均命中![]() 环,则选派谁去参加比赛更合适?请说明理由.
环,则选派谁去参加比赛更合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年10月29日党的十八届五中全会允许实行普遍二孩政策,政策规定:坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子政策,积极开展应对人口老龄化行动.然而新政策出台后,育龄妇女对生育二孩意愿并不高,为了解情况,红星社区对社区内部分妇女生二孩的意愿情况进行抽样调查,并对于其中不愿意生二孩的妇女“不愿意生二孩的原因”进行全面调查,从调查中了解到,愿意生二孩育龄妇女只有![]() 人,社区根据本次调查数据制作了相关统计图,请根据图中反映信息,回答下列问题:
人,社区根据本次调查数据制作了相关统计图,请根据图中反映信息,回答下列问题:
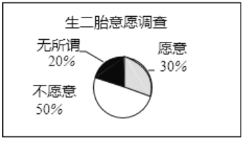
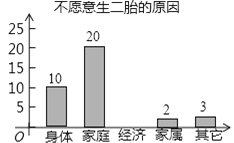
图① 图②
(1)这次调查的样本容量是 ;
(2)不愿意生二孩的育龄妇女有 人;
(3)图②为“不愿意生二孩原因”统计图,请将条形统计图补充完整;
(4)调查中了解到,由于“家属”、“其它”原因而不愿意生二孩的育龄妇女共有![]() 人,在这
人,在这![]() 人中随机抽取两人,请用树状图或列表法求出两人都是由于“家属”原因不生二孩的概率.
人中随机抽取两人,请用树状图或列表法求出两人都是由于“家属”原因不生二孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店有![]() 两种商品,已知在打折前,买
两种商品,已知在打折前,买![]() 件
件![]() 商品和
商品和![]() 件
件![]() 商品用了
商品用了![]() 元,买
元,买![]() 件
件![]() 商品和
商品和![]() 件
件![]() 商品用了
商品用了![]() 元.
元.![]() 两种商品打相同折以后,某人买
两种商品打相同折以后,某人买![]() 件
件![]() 商品和
商品和![]() 件
件![]() 商品一共比不打折少花
商品一共比不打折少花![]() 元,请问
元,请问![]() 两种商品打折前各多少钱?打了多少折?
两种商品打折前各多少钱?打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知![]() ,AC=5,那么△DBF的面积等于_____.
,AC=5,那么△DBF的面积等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB为直角,AB=10,![]() °,半径为1的动圆Q的圆心从点C出发,沿着CB方向以1个单位长度/秒的速度匀速运动,同时动点P从点B出发,沿着BA方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PB长为半径的⊙P与AB、BC的另一个交点分别为E、D,连结ED、EQ.
°,半径为1的动圆Q的圆心从点C出发,沿着CB方向以1个单位长度/秒的速度匀速运动,同时动点P从点B出发,沿着BA方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PB长为半径的⊙P与AB、BC的另一个交点分别为E、D,连结ED、EQ.
(1)判断并证明ED与BC的位置关系,并求当点Q与点D重合时t的值;
(2)当⊙P和AC相交时,设CQ为![]() ,⊙P被AC 截得的弦长为
,⊙P被AC 截得的弦长为![]() ,求
,求![]() 关于
关于![]() 的函数; 并求当⊙Q过点B时⊙P被AC截得的弦长;
的函数; 并求当⊙Q过点B时⊙P被AC截得的弦长;
(3)若⊙P与⊙Q相交,写出t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com