
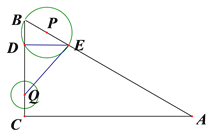
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЮЊжБНЧЃЌAB=10ЃЌ![]() ЁуЃЌАыОЖЮЊ1ЕФЖЏдВQЕФдВаФДгЕуCГіЗЂЃЌбизХCBЗНЯђвд1ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШдШЫйдЫЖЏЃЌЭЌЪБЖЏЕуPДгЕуBГіЗЂЃЌбизХBAЗНЯђвВвд1ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈ0ЃМtЁм5ЃЉвдPЮЊдВаФЃЌPBГЄЮЊАыОЖЕФЁбPгыABЁЂBCЕФСэвЛИіНЛЕуЗжБ№ЮЊEЁЂDЃЌСЌНсEDЁЂEQЃЎ
ЁуЃЌАыОЖЮЊ1ЕФЖЏдВQЕФдВаФДгЕуCГіЗЂЃЌбизХCBЗНЯђвд1ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШдШЫйдЫЖЏЃЌЭЌЪБЖЏЕуPДгЕуBГіЗЂЃЌбизХBAЗНЯђвВвд1ИіЕЅЮЛГЄЖШ/УыЕФЫйЖШдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈ0ЃМtЁм5ЃЉвдPЮЊдВаФЃЌPBГЄЮЊАыОЖЕФЁбPгыABЁЂBCЕФСэвЛИіНЛЕуЗжБ№ЮЊEЁЂDЃЌСЌНсEDЁЂEQЃЎ
ЃЈ1ЃЉХаЖЯВЂжЄУїEDгыBCЕФЮЛжУЙиЯЕЃЌВЂЧѓЕБЕуQгыЕуDжиКЯЪБtЕФжЕЃЛ
ЃЈ2ЃЉЕБЁбPКЭACЯрНЛЪБЃЌЩшCQЮЊ![]() ЃЌЁбPБЛAC НиЕУЕФЯвГЄЮЊ
ЃЌЁбPБЛAC НиЕУЕФЯвГЄЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЃЛ ВЂЧѓЕБЁбQЙ§ЕуBЪБЁбPБЛACНиЕУЕФЯвГЄЃЛ
ЕФКЏЪ§ЃЛ ВЂЧѓЕБЁбQЙ§ЕуBЪБЁбPБЛACНиЕУЕФЯвГЄЃЛ
ЃЈ3ЃЉШєЁбPгыЁбQЯрНЛЃЌаДГіtЕФШЁжЕЗЖЮЇЃЎ

ЁОД№АИЁПЃЈ1ЃЉEDЁЭBCЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉСЌНгPDЃЌгЩPB=PDЃЌPD=PEЃЌПЩЕУЁЯPBD=ЁЯPDBЃЌЁЯPDE=ЁЯPEDЃЌдйгЩШ§НЧаЮЕФФкНЧКЭЖЈРэПЩЕУЁЯBDE=ЁЯBDP+ЁЯPDE=90ЁуЃЌМДПЩЕУDEЁЭBCЃЛвђDEЁЮCAЃЌПЩЕУЁїBDEЁзЁїBCAЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪПЩЕУ![]() ЃЌЩшCQ=CD=tЃЌBD=5-tЃЌBE=2tЃЌДњШыЧѓЕУtжЕМДПЩЃЛЩшЁбPКЭACЯрНЛгк MЁЂNЃЌBP=CQ=xЃЌAP=AB-BP=10-x,Й§ЕуPзїPHЁЭACгкЕу H,дкRtЁїAPHжаЃЌПЩЕУPH=
ЃЌЩшCQ=CD=tЃЌBD=5-tЃЌBE=2tЃЌДњШыЧѓЕУtжЕМДПЩЃЛЩшЁбPКЭACЯрНЛгк MЁЂNЃЌBP=CQ=xЃЌAP=AB-BP=10-x,Й§ЕуPзїPHЁЭACгкЕу H,дкRtЁїAPHжаЃЌПЩЕУPH=![]() APЃЌPH=
APЃЌPH=![]() (10-x)ЃЌдкRtЁїPHNжаЃЌМДПЩЧѓЕУyЙигкxЕФКЏЪ§ЃЛШчЭМЃЌЕБЁбQОЙ§BЕуЪБЃЌ CQ=CBЉQB=4ЃЌНЋtЕФжЕДњШыМДПЩЧѓЕУMNЕФГЄЃЛЃЈ3ЃЉЕБQЁбPгыЁбQЭтЧаЪБЃЌШчЭМЃЌДЫЪБвзжЊЁЯQBP=60ЁуЃЌBQ=5-tЃЌPQ=t+1ЃЌBP=tЃЌ
(10-x)ЃЌдкRtЁїPHNжаЃЌМДПЩЧѓЕУyЙигкxЕФКЏЪ§ЃЛШчЭМЃЌЕБЁбQОЙ§BЕуЪБЃЌ CQ=CBЉQB=4ЃЌНЋtЕФжЕДњШыМДПЩЧѓЕУMNЕФГЄЃЛЃЈ3ЃЉЕБQЁбPгыЁбQЭтЧаЪБЃЌШчЭМЃЌДЫЪБвзжЊЁЯQBP=60ЁуЃЌBQ=5-tЃЌPQ=t+1ЃЌBP=tЃЌ![]() ЃЌвђДгДЫЪБЦ№жБжСЭЃжЙдЫЖЏЃЌЁбPгыЁбQЖМДІгкЯрНЛЮЛжУЃЌМДПЩЕУЁбPгыЁбQЯрНЛЪБtЕФШЁжЕЗЖЮЇ.
ЃЌвђДгДЫЪБЦ№жБжСЭЃжЙдЫЖЏЃЌЁбPгыЁбQЖМДІгкЯрНЛЮЛжУЃЌМДПЩЕУЁбPгыЁбQЯрНЛЪБtЕФШЁжЕЗЖЮЇ.
ЪдЬтНтЮіЃК
ЃЈ1ЃЉСЌНгPDЃЌЁпBЁЂEЁЂDЖМдкЁбPЩЯ
ЁрPB=PDЃЌЁЯPBD=ЁЯPDBЃЌ PD=PEЃЌЁЯPDE=ЁЯPED
ЁпЁїBDEЕФФкНЧКЭЮЊ180Ёу ЁрЁЯBDE=ЁЯBDP+ЁЯPDE=90ЁуЃЌ
ЁрМДЃКDEЁЭBC
ЁпЁЯBCA=90ЁуЃЌ![]() Ёу
Ёу
ЁрDEЁЮCAЃЌЁрЁїBDEЁзЁїBCAЃЌ
Ёр![]()
ЩшCQ=CD=tЃЌBD=5-tЃЌBE=2t
ДњШыга![]() НтЕУЃК
НтЕУЃК![]()
ЁрЕБ![]() ЪБQгыDжиКЯ.
ЪБQгыDжиКЯ.
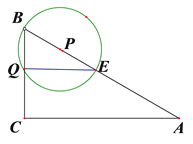
ЃЈ2ЃЉЩшЁбPКЭACЯрНЛгк MЁЂNЃЌ

BP=CQ=xЃЌAP=AB-BP=10-xЙ§ЕуPзїPHЁЭ
дкRtЁїAPHжаЃЌвзжЊЃК![]()
PH=![]()
дкRtЁїPHNжаЃЌвзжЊЃКHN=![]() =
=![]()
![]()
ЕБЁбQОЙ§BЕуЪБЃЌЃЈШчЭМЃЉ CQ=CBЉQB=4ЃЌ

НЋ![]() ДњШыЕУЃК
ДњШыЕУЃК![]()
ЃЈ3ЃЉЕБQЁбPгыЁбQЭтЧаЪБЃЌШчЭМЃЌ
взжЊДЫЪБЁЯQBP=60ЁуЃЌBQ=5-tЃЌPQ=t+1ЃЌBP=t
![]() ЃЌ
ЃЌ
ЁпДгДЫЪБЦ№жБжСЭЃжЙдЫЖЏЃЌЁбPгыЁбQЖМДІгкЯрНЛЮЛжУ
ЁрЁбPгыЁбQЯрНЛЪБtЕФШЁжЕЗЖЮЇЮЊЃК ![]()


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбјжГЛЇЕФбјжГГЩБОж№ФъдіГЄЃЌвбжЊЕквЛФъЕФбјжГГЩБОЮЊ12ЭђдЊЃЌЕк3ФъЕФбјжГГЩБОЮЊ17ЭђдЊЃЎЩшУПФъЦНОљдіГЄЕФАйЗжТЪЮЊxЃЌдђЯТУцЫљСаЗНГЬжае§ШЗЕФЪЧЃЈ ЃЉ
A.12ЃЈ1ЉxЃЉ2=17
B.17ЃЈ1ЉxЃЉ2=12
C.17ЃЈ1+xЃЉ2=12
D.12ЃЈ1+xЃЉ2=17
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЃЌНЋAЁЂBЁЂCШ§ИізжФИЫцЛњЬюаДдкШ§ИіПеИёжаЃЈУППеЬювЛИізжФИЃЌУППежаЕФзжФИВЛжиИДЃЉЃЌЧыФугУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓДгзѓЭљгвзжФИЫГађЧЁКУЪЧAЁЂBЁЂCЕФИХТЪЃЛ
ЃЈ2ЃЉШєдкШчЭМШ§ИіПеИёЕФгвВрдіМгвЛИіПеИёЃЌНЋAЁЂBЁЂCЁЂDЫФИізжФИШЮвтЬюаДЦфжаЃЈУППеЬювЛИізжФИЃЌУППежаЕФзжФИВЛжиИДЃЉЃЌДгзѓЭљгвзжФИЫГађЧЁКУЪЧAЁЂBЁЂCЁЂDЕФИХТЪЮЊ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћВЛЕШЪН![]() гаНт,ФЧУДmЕФШЁжЕЗЖЮЇЪЧ( )
гаНт,ФЧУДmЕФШЁжЕЗЖЮЇЪЧ( )
A.m>7
B.mЁн7
C.m<7
D.mЁм7
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
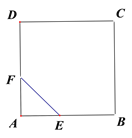
ЁОЬтФПЁПШчЭМЃЌEЁЂFЗжБ№ЮЊе§ЗНаЮABCDЕФБпABЁЂADЩЯЕФЕуЃЌЧвAE=AFЃЌСЊНгEFЃЌНЋЁїAEFШЦЕуAФцЪБеыа§зЊ45ЁуЃЌЪЙEТфдкE![]() ЃЌFТфдкF
ЃЌFТфдкF![]() ЃЌСЊНгBE
ЃЌСЊНгBE![]() ВЂбгГЄНЛDF
ВЂбгГЄНЛDF![]() гкЕуGЃЌШчЙћAB=
гкЕуGЃЌШчЙћAB=![]() ЃЌAE=1ЃЌдђDG=______.
ЃЌAE=1ЃЌдђDG=______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪЕЪ§aЃЌbТњзуЃЈ2a+1ЃЉ2+|a+b+1|=0ЃЌЧвЙигкxЃЌyЕФЗНГЬзщ![]() ЕФНтxЃМ0ЃЌyЃО0ЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЕФНтxЃМ0ЃЌyЃО0ЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКе§ЗНаЮ![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФбгГЄЯпЩЯЃЌЧв
ЕФбгГЄЯпЩЯЃЌЧв![]() .
.
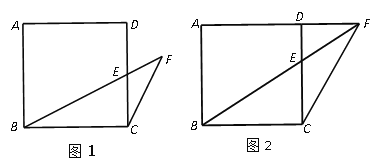
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕу![]() ЮЊ
ЮЊ![]() БпЕФжаЕуЪБЃЌЧѓжЄЃК
БпЕФжаЕуЪБЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕу![]() ЮЛгкЯпЖЮ
ЮЛгкЯпЖЮ![]() ЕФбгГЄЯпЩЯЃЌЧѓжЄЃК
ЕФбгГЄЯпЩЯЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЕуDЪЧЯвABЕФжаЕуЃЌЕуCдкЁбOЩЯЃЌCDОЙ§дВаФOЃЌдђЯТСаНсТлжаВЛвЛЖЈе§ШЗЕФЪЧЃЈ ЃЉ
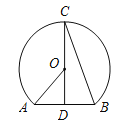
A. CDЁЭAB B. ЁЯOAD ЃН2ЁЯCBD C. ЁЯAOD ЃН2ЁЯBCD D. ЛЁAC ЃН ЛЁBC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЕФЭМЯѓЗДгГЕФЙ§ГЬЪЧЃКаЁУїДгМвШЅГЌЪаТђЮФОпЃЌгжШЅЪщЕъЙКЪщЃЌШЛКѓЛиМвЃЎЦфжаxБэЪОЪБМфЃЌyБэЪОаЁУїРыЫћМвЕФОрРыЃЌШєаЁУїМвЁЂГЌЪаЁЂЪщЕъдкЭЌвЛЬѕжБЯпЩЯЃЎ
ИљОнЭМЯѓЛиД№ЯТСаЮЪЬтЃК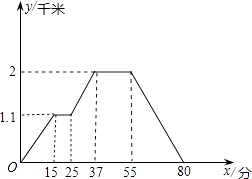
ЃЈ1ЃЉГЌЪаРыаЁУїМвЖрдЖЃЌаЁУїзпЕНГЌЪагУСЫЖрЩйЪБМфЃП
ЃЈ2ЃЉГЌЪаРыЪщЕъЖрдЖЃЌаЁУїдкЪщЕъЙКЪщгУСЫЖрЩйЪБМфЃП
ЃЈ3ЃЉЪщЕъРыаЁУїМвЖрдЖЃЌаЁУїДгЪщЕъзпЛиМвЕФЦНОљЫйЖШЪЧУПЗжжгЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com