
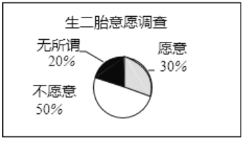
【题目】2015年10月29日党的十八届五中全会允许实行普遍二孩政策,政策规定:坚持计划生育的基本国策,完善人口发展战略,全面实施一对夫妇可生育两个孩子政策,积极开展应对人口老龄化行动.然而新政策出台后,育龄妇女对生育二孩意愿并不高,为了解情况,红星社区对社区内部分妇女生二孩的意愿情况进行抽样调查,并对于其中不愿意生二孩的妇女“不愿意生二孩的原因”进行全面调查,从调查中了解到,愿意生二孩育龄妇女只有![]() 人,社区根据本次调查数据制作了相关统计图,请根据图中反映信息,回答下列问题:
人,社区根据本次调查数据制作了相关统计图,请根据图中反映信息,回答下列问题:
图① 图②
(1)这次调查的样本容量是 ;
(2)不愿意生二孩的育龄妇女有 人;
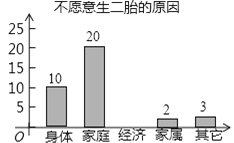
(3)图②为“不愿意生二孩原因”统计图,请将条形统计图补充完整;
(4)调查中了解到,由于“家属”、“其它”原因而不愿意生二孩的育龄妇女共有![]() 人,在这
人,在这![]() 人中随机抽取两人,请用树状图或列表法求出两人都是由于“家属”原因不生二孩的概率.
人中随机抽取两人,请用树状图或列表法求出两人都是由于“家属”原因不生二孩的概率.
【答案】(1)![]() ;
;
(2)![]() ;
;
(3)补全图形见解析;
(4)两人都是由于“家属”原因不生二孩的概率为![]() .
.
【解析】
(1)由愿意生二孩育龄妇女只有![]() 人、占总人数的
人、占总人数的![]() 可得;
可得;
(2)总人数乘以不愿意生二孩的育龄妇女所占百分比可得;
(3)用不愿意生二孩的人数减去另外四个原因的人数即可求得“经济”的人数,从而补全图形;
(4)用![]() 表示“家属”原因,用
表示“家属”原因,用![]() 表示“其它”原因,画树状图得出所有结果数,再利用概率公式求解可得.
表示“其它”原因,画树状图得出所有结果数,再利用概率公式求解可得.
解:(1)这次调查的样本容量是![]() ,
,
故答案为:![]() ;
;
(2)不愿意生二孩的育龄妇女有![]() 人,
人,
故答案为:![]() ;
;
(3)由于“经济”原因的人数为![]() ,
,
补全图形如下:
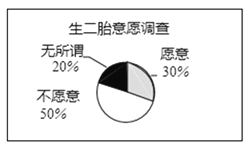
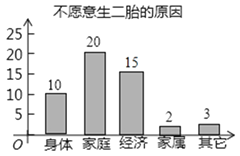
图① 图②
(4)用![]() 表示“家属”原因,用
表示“家属”原因,用![]() 表示“其它”原因,
表示“其它”原因,
画树状图如下:
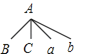
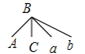
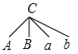
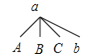
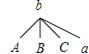
由树状图可知,所有等可能的结果为![]() 种,其中两人都是“家属”原因不愿意生二孩的有
种,其中两人都是“家属”原因不愿意生二孩的有![]() 种,
种,
所以两人都是由于“家属”原因不生二孩的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数![]() 上一个动点,
上一个动点,![]() 轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会
轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会![]()
![]()
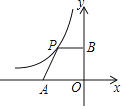
A. 先增后减 B. 先减后增 C. 逐渐减小 D. 逐渐增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() 和点
和点![]() ,与
,与![]() 轴的交点为
轴的交点为![]() .
.
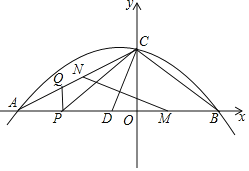
(1)求抛物线的解析式;
(2)点![]() 是线段
是线段![]() 上一动点(不与点
上一动点(不与点![]() 重合),过
重合),过![]() 作平行于
作平行于![]() 轴的直线与
轴的直线与![]() 交于点
交于点![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上.
上.
①是否同时存在点![]() 和点
和点![]() ,使得
,使得![]() 和
和![]() 全等,若存在,求点
全等,若存在,求点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
②若![]() ,
,![]() 是
是![]() 的垂直平分线,求点
的垂直平分线,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 边上的两动点,且在运动过程中保持
边上的两动点,且在运动过程中保持![]() ,
,![]() 为
为![]() 的对角线.
的对角线.
(1)如图①,若![]() ,
,

图①
①当点![]() 与点
与点![]() 重合时,探索
重合时,探索![]() 的值;
的值;
②当点![]() 与点
与点![]() 不重合时,探索
不重合时,探索![]() 的值;
的值;
(2)如图②,参考(1)研究方法,若![]() ,
,

图②
①当点![]() 与点
与点![]() 重合时,探索
重合时,探索![]() 的值;
的值;
②当点![]() 与点
与点![]() 不重合时,探索
不重合时,探索![]() 的值;
的值;
(3)如图③,参考(1)(2)研究方法,若![]() 时,试探索是否存在常数
时,试探索是否存在常数![]() ,使得
,使得![]() ,若存在,请直接写出
,若存在,请直接写出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B分别在反比例函数![]() (x>0),
(x>0),![]() (k<0,x>0)的图象上.点B的横坐标为4,且点B在直线y=x﹣5上.
(k<0,x>0)的图象上.点B的横坐标为4,且点B在直线y=x﹣5上.
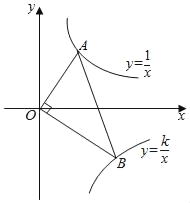
(1)求k的值;(2)若OA⊥OB,求tan∠ABO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设![]() (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为
(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为![]() 千米,骑自行车学生骑行的路程为
千米,骑自行车学生骑行的路程为![]() 千米,
千米,![]() 关于
关于![]() 的函数图象如图所示.
的函数图象如图所示.
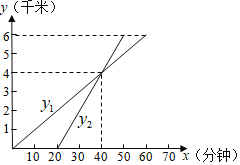
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣(2m+1)x+m2+m,其中m是常数.
(1)求证:不论m为何值,该抛物线与z轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=![]() ,请求出该抛物线的顶点坐标.
,请求出该抛物线的顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com