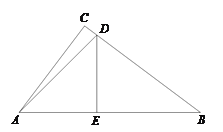
【题目】如图，在Rt△ABC中，
，点
在边
上，
⊥
，点
为垂足，
，∠DAB=450，tanB=
.
(1)求的长；
(2)求
的余弦值．
【答案】(1)3;(2)
【解析】分析：（1）由题意得到三角形ADE为等腰直角三角形，在直角三角形DEB中，利用锐角三角函数定义求出DE与BE之比，设出DE与BE，由AB=7求出各自的值，确定出DE即可；
（2）在直角三角形中，利用勾股定理求出AD与BD的长，根据tanB的值求出cosB的值，确定出BC的长，由BC﹣BD求出CD的长，利用锐角三角函数定义求出所求即可．
详解：（1）∵DE⊥AB，∴∠DEA=90°．又∵∠DAB=45°，∴DE=AE．在Rt△DEB中，∠DEB=90°，tanB=
=
，设DE=3x，那么AE=3x，BE=4x．∵AB=7，∴3x+4x=7，解得：x=1，∴DE=3；
（2）在Rt△ADE中，由勾股定理，得：AD=3
，同理得：BD=5．在Rt△ABC中，由tanB=，可得：cosB=
，∴BC=
，∴CD=
，∴cos∠CDA=
=，即∠CDA的余弦值为．
科目：初中数学 来源： 题型：
【题目】实验室里，水平桌面上有甲、乙、丙三个相同高度的圆柱形容器（容器足够高），底面积之比为
，用两个相同的管子在
高度处连通（即管子底部离容器底），现三个容器中，只有甲中有水，水位高
，如图所示. 若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升
.
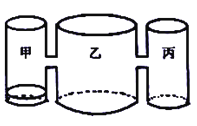
（1）开始注水1分钟，丙的水位上升__________
；
（2）求出开始注入多少分钟的水量后，甲与乙的高度之差是
？
查看答案和解析>>
科目：初中数学 来源： 题型：
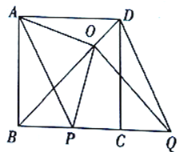
【题目】如图，
是正方形
的对角线，
.边
在其所在的直线上平移，将通过平移得到的线段记为
，连接
、
，并过点
作
，垂足为
，连接
、
.
(1)请直接写出线段在平移过程中，四边形
是什么四边形；
(2)请判断、之间的数量关系和位置关系，并加以证明；
(3)在平移变换过程中，设
，
，求
与
之间的函数关系式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】电话计费问题
下表中有两种移动电话计费方式方式
月使用费/元 | 主叫限定 时间/min | 主叫超时 费/（元/min） | 被叫 | |
方式一 | 50 | 120 | 0.2 | 免费 |
方式二 | 80 | 300 | 0.1 | 免费 |
解决问题：
（1）设一个月内使用移动电话主叫时间为t分钟（为正整数）．根据上表信息填写下表：
主叫时间t（分钟） | 方式一计费（元） | 方式二计费（元） |
| 50 | 80 |
| ||
|
（2）如果王刚每月打电话的主叫时间t不超过500分钟，请你帮助他分析选择一种省钱的计费方式，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】周末，小明和爸爸在400米的环形跑道上骑车锻炼，他们在同一地点沿着同一方向同时出发，骑行结束后两人有如下对话：
（1）他们的对话内容，求小明和爸爸的骑行速度，
（2）一次追上小明后，在第二次相遇前，再经过多少分钟，小明和爸爸相距50m？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（ ）
A. 
B. 1 C. 
D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC．
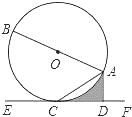
（1）求证：EF是⊙O的切线；
（2）若⊙O的半径为2，∠ACD=30°，求图中阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
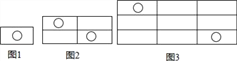
【题目】如图所示，图（1）中含“○”的矩形有1个，图（2）中含“○”的矩形有7个，图（3）中含“○”的矩形有17个，按此规律，图（6）中含“○”的矩形有（ ）
A. 70 B. 71 C. 72 D. 73
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
