
【题目】实验室里,水平桌面上有甲、乙、丙三个相同高度的圆柱形容器(容器足够高),底面积之比为![]() ,用两个相同的管子在
,用两个相同的管子在![]() 高度处连通(即管子底部离容器底
高度处连通(即管子底部离容器底![]() ),现三个容器中,只有甲中有水,水位高
),现三个容器中,只有甲中有水,水位高![]() ,如图所示. 若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升
,如图所示. 若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() .
.
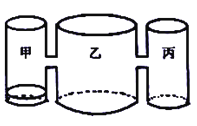
(1)开始注水1分钟,丙的水位上升__________![]() ;
;
(2)求出开始注入多少分钟的水量后,甲与乙的高度之差是![]() ?
?
【答案】(1)![]() ;(2)
;(2)![]() 分钟或
分钟或![]() 分钟或
分钟或![]() 分钟.
分钟.
【解析】
(1)乙、丙两个圆柱形容器底面面积之比为3:1,乙的水位上升![]() ,可求出丙上升的高度为
,可求出丙上升的高度为![]() ;
;
(2)分四种情况讨论.①甲的高度高于乙的高度0.5cm;②丙、乙都未达6cm时,乙的高度高于甲的高度0.5cm;③丙到达6cm而乙未达6cm时,乙的高度高于甲的高度0.5cm;④丙、乙都到达6cm后,乙的高度高于甲的高度0.5cm.
解:(1)由题意知,乙、丙两个圆柱形容器底面面积之比为3:1,丙的水位上升![]() ,
,
∴开始注水1分钟,丙容器的水位上升了![]()
![]() .
.
(2)设开始注入x分钟的水量后,甲与乙的水位高度之差是0.5cm.由题意分为四种情况:
①甲的高度高于乙的高度0.5cm,则:![]() ,解得
,解得![]() .
.![]()
②丙、乙都未达6cm时,乙的高度高于甲的高度0.5cm,
![]() ,解得
,解得![]() .
.![]()
③丙到达6cm而乙未达6cm时,乙的高度高于甲的高度0.5cm.因为乙未到达6cm,所以甲的高度不变,而乙的高度在不断上升,故此种情况不符合题意;
④丙、乙都到达6cm后,乙的高度高于甲的高度0.5cm.设乙都到达6cm的时间为y分钟,
∵丙到达6cm时的时间为![]() 分钟,
分钟,
∴![]() ,
,
解得,![]() ,
,
∴![]() ,
,
解得,![]() ,
,
综上所述,当开始注入![]() 分钟或
分钟或![]() 分钟或
分钟或![]() 分钟水量后,甲与乙的高度之差是
分钟水量后,甲与乙的高度之差是![]() .
.


科目:初中数学 来源: 题型:
【题目】某校八年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛.各参赛选手成绩的数据分析如下表所示,则以下判断错误的是( )
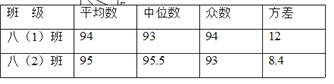
A. 八(2)班的总分高于八(1)班 B. 八(2)班的成绩比八(1)班稳定
C. 八(2)班的成绩集中在中上游 D. 两个班的最高分在八(2)班
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 与
与![]() 的图象如图所示,则下列结论①k<0;②a>0;③不等式x+a<kx+b的解集是x<3;④ab=3k3中,正确的个数是()
的图象如图所示,则下列结论①k<0;②a>0;③不等式x+a<kx+b的解集是x<3;④ab=3k3中,正确的个数是()

A. 3个B. 2个C. 1个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张大小相同的长方形卡片(如图①)按图②、图③两种放法放在一个底面为长方形(长为![]() ,宽为
,宽为![]() )的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为
)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为![]() ,图③中阴影部分的周长为
,图③中阴影部分的周长为![]() ,则
,则![]() ___________.
___________.
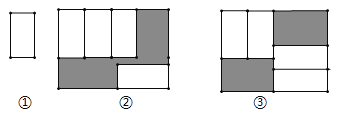
查看答案和解析>>
科目:初中数学 来源: 题型:
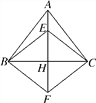
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,点A(-4,0),点B在直线y=x+2上.当A、B两点间的距离最小时,点B的坐标是( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (-3,-1) D. (-3,
) C. (-3,-1) D. (-3,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线L与y=2x+1的交于点A(2,a),与直线y=x+2的交于点B(b,1)
(1)求a,b的值;
(2)求直线l的函数表达式;
(3)求直线L、x轴、直线y=2x+1围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com