
【题目】已知,在平面直角坐标系xOy中,点A(-4,0),点B在直线y=x+2上.当A、B两点间的距离最小时,点B的坐标是( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (-3,-1) D. (-3,
) C. (-3,-1) D. (-3,![]() )
)
科目:初中数学 来源: 题型:
【题目】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示. 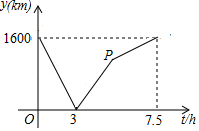
(1)填空:动车甲的速度为(km/h),动车乙的速度为(km/h);
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)两车何时相距1200km?
查看答案和解析>>
科目:初中数学 来源: 题型:
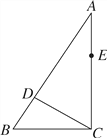
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
(1)若乐乐这个月平均每天健步走的步数为1.32万步,试求她走1.3万步和1.5万步的天数;
(2)求这组数据中的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
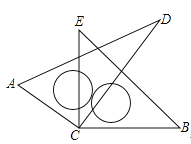
【题目】如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=120°,求∠DCE的度数.
(3)猜想∠ACB和∠DCE的关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.
(1)如图1,若∠1=60°,求∠2,∠3的度数.

(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD请阅读下面的解答过程并填空(理由或数学式)
解:如图2,过点P作MN∥AB
则∠EPM=∠PEB(_______)
∵AB∥CD(已知)MN∥AB(作图)
∴MN∥CD(_______)
∴∠MPF=∠PFD (_______)
∴_____=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
②拓展应用,当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=_____度.
③当点P在图4的位置时,请直接写出∠EPF,∠PEB,∠PFD三个角之间关系_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商家常将两种糖混合成“什锦糖”出售.对“什锦糖”的定价用以下方法确定:
若A种糖的单价为a元/千克,B种糖的单价为b元/千克(a≠b),则m千克的A种糖与n千克的B种糖混合而成的“什锦糖”单价为![]() 元.
元.
(1)当a=20,b=30时,
①将10千克的A种糖与15千克的B种糖混合而成的“什锦糖”单价为多少?
②在①的基础上,若要将“什锦糖”单价提高2元,则需增加B种糖多少千克?
(2)若现有两种“什锦糖”:一种是由10千克的A种糖和10千克的B种糖混合而成,另一种是由100元价值的A种糖和100元价值的B种糖混合而成,则这两种“什锦糖”的单价哪一种更大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了节约用水,对自来水的收费标准作如下规定:每月每户用水不超过10吨的部分,按2元/吨收费;超过10吨的部分按2.5元/吨收费.
(1)若黄老师家5月份用水16吨,问应交水费多少元?
(2)若黄老师家6月份交水费30元,问黄老师家5月份用水多少吨?
(3)若黄老师家7月用水a吨,问应交水费多少元?(用a的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com