
����Ŀ����ͼ����֪��ABC�У�AB��AC��5��BC��6����O�DZ�BC�ϵĶ��㣬�Ե�OΪԲ�ģ�OBΪ�뾶��ԲO����AB���ڵ�D������D����ODP����B������AC�ڵ�P����ԲO���E����OB��x��
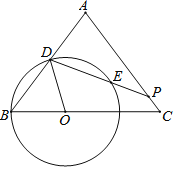
��1������P���C�غ�ʱ����PD�ij���
��2����AP��EP��y����y����x�Ľ���ʽ��������
��3������OP����OP��ODʱ�����ж��Ե�PΪԲ�ģ�PCΪ�뾶��ԲP��ԲO��λ�ù�ϵ��
���𰸡���1��5����2��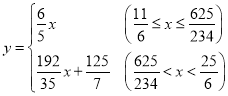 ����3���Ե�PΪԲ�ģ�PCΪ�뾶��ԲP��ԲO��λ�ù�ϵ���ཻ
����3���Ե�PΪԲ�ģ�PCΪ�뾶��ԲP��ԲO��λ�ù�ϵ���ཻ
��������
��1������OB=OD��AB=AC�Լ���ADO=��B+��BOD=��ODP+��ADP�����Ŀ������ODP=��B���������
��2���ֵ�P��C�غϣ�P��E�غϣ�D��A�غ�����������ۣ������Ӧ��xֵ���ٷ���������ֱ������Ӧ�Ľ���ʽ
��3������OP�������Բ�İ뾶��Բ�ľ༴���ж���Բ��λ�ù�ϵ
��1����ͼ1�У���AH��BC��H��CG��AB��G��
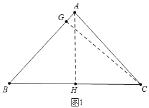
��AB��AC��5��AH��BC��
��BH��CH��3��AH��4��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��ͼ2�У�����P��C�غ�ʱ��
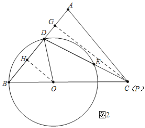
��OB��OD��
���B����ODB����ACB��
�ߡ�ADO����B+��BOD����CDO+��ADP����ODP����B��
���ADP����BOD����BAC��
��PA��PD��5��
���ⷨ����֪��A��180�㩁2��B��ֻҪ֤����ADP��180�㩁2��B���ɽ�����⣩
��2����ͼ2�У���CG��AB��G��OH��BD��H��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��ͼ3�У���P��E�غ�ʱ����EG��AD��G��
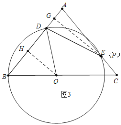
���ݶԳ��Կ�֪��B��E����ֱ��OD�Գƣ�
��![]() ��
��
��![]() ��
��
��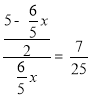 ��
��
���![]() ��
��
����D��A�غ�ʱ![]() ��
��
��![]() ��
��
��![]() ʱ����ͼ4�У�
ʱ����ͼ4�У�
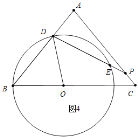
��![]() ��
��
��![]() ��
��
��![]() ʱ����ͼ5�У���PG��AB��G��
ʱ����ͼ5�У���PG��AB��G��
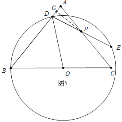
��![]() ��
��
��![]() ��
��
��![]() ��
��
����������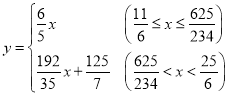 ��
��
��3����ͼ6�У�����OP��
����OP����DK��OB��ON��BD��PM��BC��M����ON��4k������֪OB��DO��5k��BN��DN��3k��
![]() ��
��
�ɡ�DOK�ס�OPM�ɵ�![]() ���ɵ�
���ɵ�![]() ��
��
��![]() k��
k��
���Ե�PΪԲ�ģ�PCΪ�뾶��ԲP��ԲO��λ�ù�ϵ���ཻ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѡ������˶�Ա�μӱ������ס�����������ͬ��������������и�![]() �Σ����еĻ�������Ϊ������10���������������
�Σ����еĻ�������Ϊ������10���������������
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�� |
|
|
|
|
|
|
|
|
|
|
�� |
|
|
|
|
|
|
|
|
|
|
��1����![]() Ϊ��ֵʱ��ѡ����ȥ�μӱ��������ʣ���˵�����ɣ�
Ϊ��ֵʱ��ѡ����ȥ�μӱ��������ʣ���˵�����ɣ�
��2���������������о�����![]() ������ѡ��˭ȥ�μӱ��������ʣ���˵�����ɣ�
������ѡ��˭ȥ�μӱ��������ʣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�B����ʱ�뷽����ת�õ���EBD����E����D�ֱ����A����C��Ӧ���ҵ�D�ڱ�AC�ϣ���DE����AB�ڵ�F����BDC�ס�ABC����֪![]() ��AC��5����ô��DBF���������_____��
��AC��5����ô��DBF���������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ���г��ļס��������̵��ж�������ij��ˮ������������ˮ��xǧ��ʱ���ڼס��������̵�������Ǯ�ֱ�Ϊy1Ԫ��y2Ԫ����֪y1��y2����x�ĺ���ͼ��ֱ�Ϊ��ͼ��ʾ������OAB������OC��

��1����x��ȡֵΪ�� ��ʱ���ڼ������ҵ�����Ǯһ���ࣿ
��2����x��ȡֵΪ�� ��ʱ�����ҵ������Ƚϱ��ˣ�
��3���������30ǧ�˸�ˮ��ʱ���ڼ����������ҵ���������50Ԫ��������AB�ı���ʽ����д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
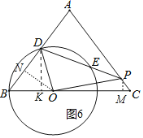
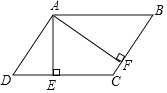
����Ŀ����ͼ����ƽ���ı���ABCD�У�AE��CD������ΪE��AF��BC������ΪF��AD��4��BF��3����EAF��60������![]() ���������
���������![]() ����ôk��ֵ��_____��
����ôk��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
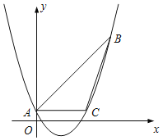
����Ŀ����ͼ����֪������y��ax2��2x+c������ABC���������㣬���е�A(0��1)����B(9��10)��AC��x�ᣮ
(1)�����������ߵĽ���ʽ.
(2)��tan��ABC��ֵ.
(3)����DΪ�����ߵĶ��㣬��E��ֱ��AC��һ�㣬����CDE���ABC����ʱ�����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACBΪֱ�ǣ�AB=10��![]() �㣬�뾶Ϊ1�Ķ�ԲQ��Բ�Ĵӵ�C����������CB������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�B����������BA����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5����PΪԲ�ģ�PB��Ϊ�뾶�ġ�P��AB��BC����һ������ֱ�ΪE��D������ED��EQ��
�㣬�뾶Ϊ1�Ķ�ԲQ��Բ�Ĵӵ�C����������CB������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�B����������BA����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5����PΪԲ�ģ�PB��Ϊ�뾶�ġ�P��AB��BC����һ������ֱ�ΪE��D������ED��EQ��
��1���жϲ�֤��ED��BC��λ�ù�ϵ������Q���D�غ�ʱt��ֵ��
��2������P��AC�ཻʱ����CQΪ![]() ����P��AC �صõ��ҳ�Ϊ
����P��AC �صõ��ҳ�Ϊ![]() ����
����![]() ����
����![]() �ĺ����� ����Q����Bʱ��P��AC�صõ��ҳ���
�ĺ����� ����Q����Bʱ��P��AC�صõ��ҳ���
��3������P���Q�ཻ��д��t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ���E��AD���ϣ���F��AD���ӳ����ϣ���BE=CF��
��1����֤���ı���EBCF��ƽ���ı��Σ�
��2������BEC=90�㣬��ABE=30�㣬AB=![]() ����ED�ij���
����ED�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������˿��ƣ�������ȫ��ͬ�������˿��Ʊ��泯�ϣ�ϴ�Ⱥ���������ϼף������˽���������Ϸ�����ȴ��������ȡһ�ţ����������ٷŻ�ϴ�ȣ����ٴ��������ȡһ�ţ�

��1���׳鵽������������һ�¼����� ���¼������������������������������Ȼ������
��2��������״ͼ���б��ķ�������������˳鵽ͬһ���˿��Ƶĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com