
【题目】如图,已知,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,以点
边上,以点![]() 为圆心
为圆心![]() 为半径作弧交边
为半径作弧交边![]() 于点
于点![]() ,射线
,射线![]() 与射线
与射线![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的长;
的长;
(2)联结![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得△
,使得△![]() 与△
与△![]() 相似,若相似,求
相似,若相似,求![]() 的值,若不相似,请说明理由
的值,若不相似,请说明理由
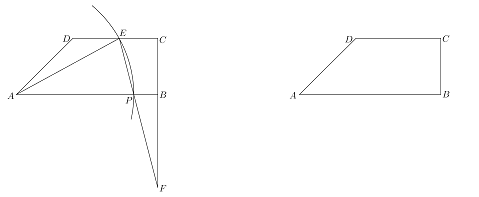
【答案】(1)1;(2)![]() ;(3)存在,FG=3
;(3)存在,FG=3![]() -1
-1
【解析】
(1)如图所示,作DO⊥AB,垂足为O,先求出DO的长,然后根据勾股定理可求出DE的长;(2)如图作EQ⊥AB,垂足为Q,先根据HL证明Rt△EQP≌Rt△CBP,得到PB=PQ,设PB=x,则PQ=x,AP=5-x,根据勾股定理列一元二次方程,求解即可;(3)先根据三角形相似求出∠EAB的大小,然后根据特殊角的三角函数求出AD、DE、GD的长,再根据相似三角形对应边成比例即可求出FG的长.
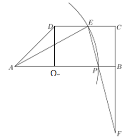
(1)如图所示,作DO⊥AB,垂足为O.
∵DC=3,AB=5,
∴AO=2,
又∵∠A=45°,∴DO=2,
依题意易知,AE=AP=![]() ,
,
根据勾股定理,AE2=(AO+DE)2+DO2,即(2+DE)2+4=13,
解得DE=﹣5(舍去)或1,
∴DE=1,
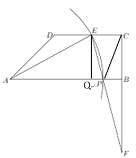
(2)如图作EQ⊥AB,垂足为Q.
∵CP=EP,EQ=CB,∴Rt△EQP≌Rt△CBP,
∴PB=PQ,
设PB=x,则PQ=x,AP=5-x,
由(1)知CB=EQ=2,
又∵AE=AP=5-x,
根据勾股定理有AE2=AQ2+EQ2,即(5-x)2=(5-2x)2+4,
解得x=![]() 或
或![]() ,
,
∴AP=![]() (<AD,舍去)或
(<AD,舍去)或![]() ,
,
综上,AP=![]() .
.
(3)∵∠F+∠FPB=90°,∠EAB+2∠APE=180°,∠APE=∠FPB,
∴∠EAB=2∠F,
若存在三角形相似,则∠DAE=∠F,
又∵∠A=45°,∴∠EAB=30°,
如图所示,延长CD,作AH⊥CD,垂足为H,
AH=DH=2,EH=2![]() ,
,
∴DE=2![]() -2,CE=5-2
-2,CE=5-2![]() ,
,
∵∠EGF=∠ADE=135°,
∴∠EGC=45°,
∴EG=![]() CE=5
CE=5![]() ,
,
∵△ADE∽△FGE,
∴![]() ,即
,即![]() ,
,
∴FG=3![]() -1.
-1.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
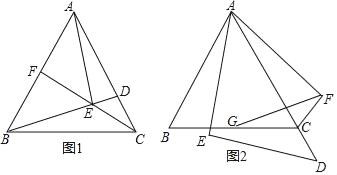
【题目】如图,在等边△ABC中,点D是AC边上一点,连接BD,过点A作AE⊥BD于E.
(1)如图1,连接CE并延长CE交AB于点F,若∠CBD=15°,AB=4,求CE的长;
(2)如图2,当点D在线段AC的延长线上时,将线段AE绕点A逆时针旋转60°得到线段AF,连接EF,交BC于G,连接CF,求证:BG=CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,这个三角形面积S最大?最大面积是多少?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
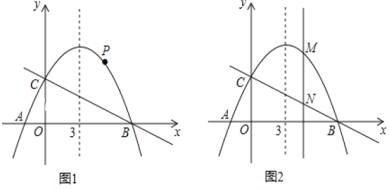
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
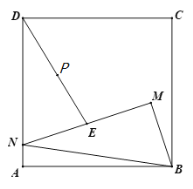
【题目】如图,M为正方形ABCD内一点,点N在AD边上,且∠BMN=90°,MN=2MB.点E为MN的中点,点P为DE的中点,连接MP并延长到点F,使得PF=PM,连接DF.
(1)依题意补全图形;
(2)求证:DF=BM;
(3)连接AM,用等式表示线段PM和AM的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳某公司销售统计了每个销售员在某月的销售额,绘制了如下折线统计图和扇形统计图: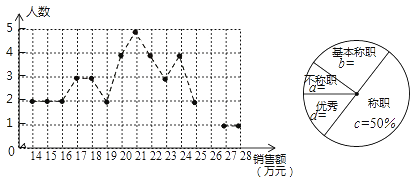
设销售员的月销售额为x(单位:万元)。销售部规定:当x<16时,为“不称职”,当 ![]() 时为“基本称职”,当
时为“基本称职”,当![]() 时为“称职”,当
时为“称职”,当![]() 时为“优秀”.根据以上信息,解答下列问题:
时为“优秀”.根据以上信息,解答下列问题:
(1)补全折线统计图和扇形统计图;
(2)求所有“称职”和“优秀”的销售员销售额的中位数和众数;
(3)为了调动销售员的积极性,销售部决定制定一个月销售额奖励标准,凡月销售额达到或超过这个标准的销售员将获得奖励。如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖,月销售额奖励标准应定为多少万元(结果去整数)?并简述其理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
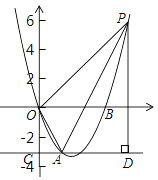
【题目】如图,已知抛物线![]() 过点A(
过点A(![]() ,-3) 和B(3
,-3) 和B(3![]() ,0),过点A作直线AC//x轴,交y轴与点C.
,0),过点A作直线AC//x轴,交y轴与点C.
(1)求抛物线的解析式;
(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D,连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;
(3)抛物线上是否存在点Q,使得![]() ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
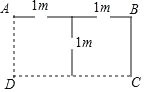
【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com