
【题目】解方程:
(1) 2x2-x=0
(2) x2-4x=4
(3) 6x+9=2x2
(4) 4y2-4y-2=0
【答案】(1) x1=0,x2=![]() ;(2) x1=2+2
;(2) x1=2+2![]() ,x2=2-2
,x2=2-2![]() ;(3)
;(3) ![]() ;(4)
;(4) ![]()
【解析】
(1)把方程左边提公因式分解因式可得![]() ,进而可得两个一元一次方程x=0或2x-1=0,再解即可;
,进而可得两个一元一次方程x=0或2x-1=0,再解即可;
(2)方程两边同时加上4,可得(x-2)2=8,再开方即可;
(3)首先移项6x+9=2x2,然后将二次项系数化为1,配方可得(x-![]() )2=
)2=![]() ,再开方即可求;
,再开方即可求;
(4)先计算出b2-4ac,再利用求根公式即可解得.
(1)解:2x2-x=0,x(2x-1)=0,x=0或2x-1=0, 则x1=0,x2=![]() .
.
(2)解:方程两边同时+4,得x2-4x+4=4+4,(x-2)2=8,
根据平方根的意义,得x-2=±2 ![]() ,
,
∴x1=2+2![]() ,x2=2-2
,x2=2-2![]() .
.
(3)移项,得2x2-6x-9=0.
将二次项系数化为1,得x2-3x-![]() =0.
=0.
配方,得x2-3x+(![]() )2-(
)2-(![]() )2-
)2-![]() =0,
=0,
(x-![]() )2=
)2=![]() .
.
根据平方根的意义,得x-![]() =±
=±![]() ,
,
∴x1=![]() ,x2=
,x2=![]() .
.
(4)4y2-4y-2=0.
∵a=4,b=-4,c=-2,
∴b2-4ac=(-4)2-4×4×(-2)=48,
∴y=![]() =
=![]() ,
,
∴y1=![]() ,y2=
,y2=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将一块腰长为![]() 的等腰直角三角板ABC放在平面直角坐标系中,点A在y轴正半轴上,直角顶点C的坐标为(2,0),点B在第二象限.
的等腰直角三角板ABC放在平面直角坐标系中,点A在y轴正半轴上,直角顶点C的坐标为(2,0),点B在第二象限.
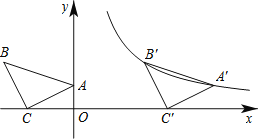
(1)求点A,点B的坐标;
(2)将△ABC沿x轴正方向平移后得到△A′B′C′,点A′,B′恰好落在反比例函数![]() 的图象上,求平移的距离和反比例函数的解析式.
的图象上,求平移的距离和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
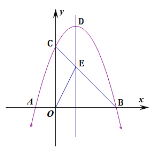
(1)求此抛物线的解析式.
(2)若点P在第一象限内的抛物线上,且S△PAB=S△OEB,求点P的横坐标.
(3)将△OBE以点B为中心顺时针旋转,旋转角等于2∠OBC,设点E的对应点为点E',点O的对应点为点O',求直线O'E'与抛物线的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将小球沿地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度![]() (
(![]() )与它的飞行时间
)与它的飞行时间![]() (
(![]() )满足二次函数关系,
)满足二次函数关系,![]() 与
与![]() 的几组对应值如下表所示:
的几组对应值如下表所示:

|
|
|
|
|
| … |
|
|
|
|
|
| … |
(1)求![]() 关于
关于![]() 的函数解析式(不要求写
的函数解析式(不要求写![]() 的取值范围)
的取值范围)
(2)问:小球的飞行高度能否达到![]() ?请说明理由
?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=9,点C为线段AB上一点,AC=3,点D为平面内一动点,且满足CD=3,连接BD将BD绕点D逆时针旋转90到DE,连接BE、AE,则AE的最大值为 ________。
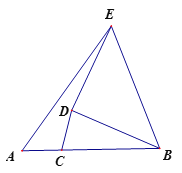
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(
的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(![]() ,y1),(
,y1),(![]() ,y2)是抛物线上两点,则y1<y2,其中正确的结论有( )个
,y2)是抛物线上两点,则y1<y2,其中正确的结论有( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=![]() ,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F.
(1)求∠EAD的余切值;
(2)求![]() 的值.
的值.
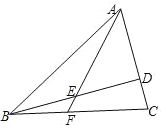
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com